Logistic Regression (1)

이번 포스트에서는 logistic regression에 대해서 알아보도록 하겠습니다.

1) Notation

앞으로 모형을 설명할 때 사용할 변수와 관측값을 다음과 같이 정의를 하겠습니다.

• $(\boldsymbol x, \boldsymbol y)$ : $\boldsymbol x \in \mathbb R^{n_x}$ : feature, $\boldsymbol y \in \mathbb R^{n_y}$ : Outcome입니다.

• ${(\boldsymbol x^{(1)}, \boldsymbol y^{(1)}), …, (\boldsymbol x^{(m)}, \boldsymbol y^{(m)})}$ : $m$개의 training example입니다. 위첨자에 $()$를 이용하여 정의합니다.

• $m$개의 train data, $M$개의 test data가 존재합니다.

• 해당 training example을 하나의 matrix로 만들 수 있습니다. 다음과 같이 \(X = \begin{bmatrix}\boldsymbol x^{(1)} & \boldsymbol x^{(2)}&...&\boldsymbol x^{(m)} \end{bmatrix}\) 만들 수 있으며, 해당 matrix의 size는 $\boldsymbol n_x \times m$입니다. 또한, $\boldsymbol y$ 또한 matrix로 \(Y = \begin{bmatrix}\boldsymbol y^{(1)} & \boldsymbol y^{(2)} & ... & \boldsymbol y^{(m)} \end{bmatrix}\) 만들 수 있습니다. 이 때 $Y$는 $ n_y \times m$ matrix입니다.

2) Logistic Regression

(1) Types of Machine learning problem

머신러닝에서 다루는 문제를 크게 Supervised Learning, Unsupervised learning으로 구분합니다.

• Supervised Learning

  데이터가 주어질 때 설명변수(feature, explanatory variable)과 반응변수(outcome, response variable)이 주어지는 문제입니다. Outcome의 종류에 따라 regression과 classfication으로 구분합니다.

  • Regression

    Outcome 값이 연속적인 값을 가질 때 Regression 문제라고 합니다. 집 값 예측 문제, 주식 가격 예측 문제 등이 regression 문제에 해당합니다.

  • Classification

    Outcome 값이 범주형 값을 가질 때 Classification 문제라고 합니다. 사진이 고양이인지 아닌지 예측하기, 특정 질병 유무 예측하기 등이 classfication 문제에 해당합니다.

• Unsupervised Learning

  데이터가 주어질 때 feature만 주어지는 문제입니다. 맞추어야 할 값인 outcome이 없기 때문에, 데이터의 feature 분포를 통해 데이터의 특징을 찾아내는 작업을 진행합니다.

이 중 supervised learning 중 classification 문제에서, outcome이 가질 수 있는 값이 2개인 문제에서 사용하는 모델 중 하나가 logistic regression입니다.

(2) Logistic Regression

Outcome이 가질 수 있는 값이 2개(Binary)일 때, logistic regression을 생각해볼 수 있습니다. Classification 문제에서, feature 값을 이용하여 해당 observation의 $y$값이 무엇인지 확인하려면, $y$가 가질 수 있는 label 각각에 대한 확률을 확인해보아야 합니다. 즉

\[P(y = 1 \mid x), P(y=0 \mid x)\]

두 확률을 구한 뒤, 확률값이 큰 label을 예측값으로 도출할 수 있습니다. 즉, 데이터가 주어졌을 때, outcome label을 가질 확률을 모델링함으로써 outcome값을 예측 또는 추정할 수 있습니다. 이 때, 무턱대고 다음과 같이

\[P(y=1 \mid x) = \beta_0 + \beta_1x\]

와 같이 선형식으로 작성하게 되면 문제가 발생합니다. 이는 $x$의 값이 연속이라면, $\beta_1$이 0이 아닌 이상 $\beta_0+\beta_1 x$가 가질 수 있는 값은 실수 전체값입니다. 하지만 $P(y=1 \mid x)$는 확률값이기 때문에, 0과 1의 값 사이에서 정의되어야 합니다. 즉, 선형식으로 작성하게 되면 $x$값에 따라 확률 범위를 벗어나 문제가 발생할 수 있습니다.

따라서 우변의 식에 특정한 함수를 합성시켜 치역값이 0과 1 사이의 값이 되도록 조정을 해줍니다. Logistic regression에서 조정해주는 함수를 sigmoid 함수라고 합니다.(통계에서는 expit 함수라고 합니다.)

\[\sigma(x) = \frac{\exp(x)}{1+\exp(x)}\]

만약 $x$값이 무한히 커진다면($\infty$), $\sigma(x)$의 값은 1로 수렴합니다. 한편, $x$값이 무한히 작아진다면($-\infty$), $\sigma(x)$의 값은 0으로 수렴합니다. 그리고 $x$가 0일 때, $\sigma(0)=\frac{1}{2}$가 됩니다.

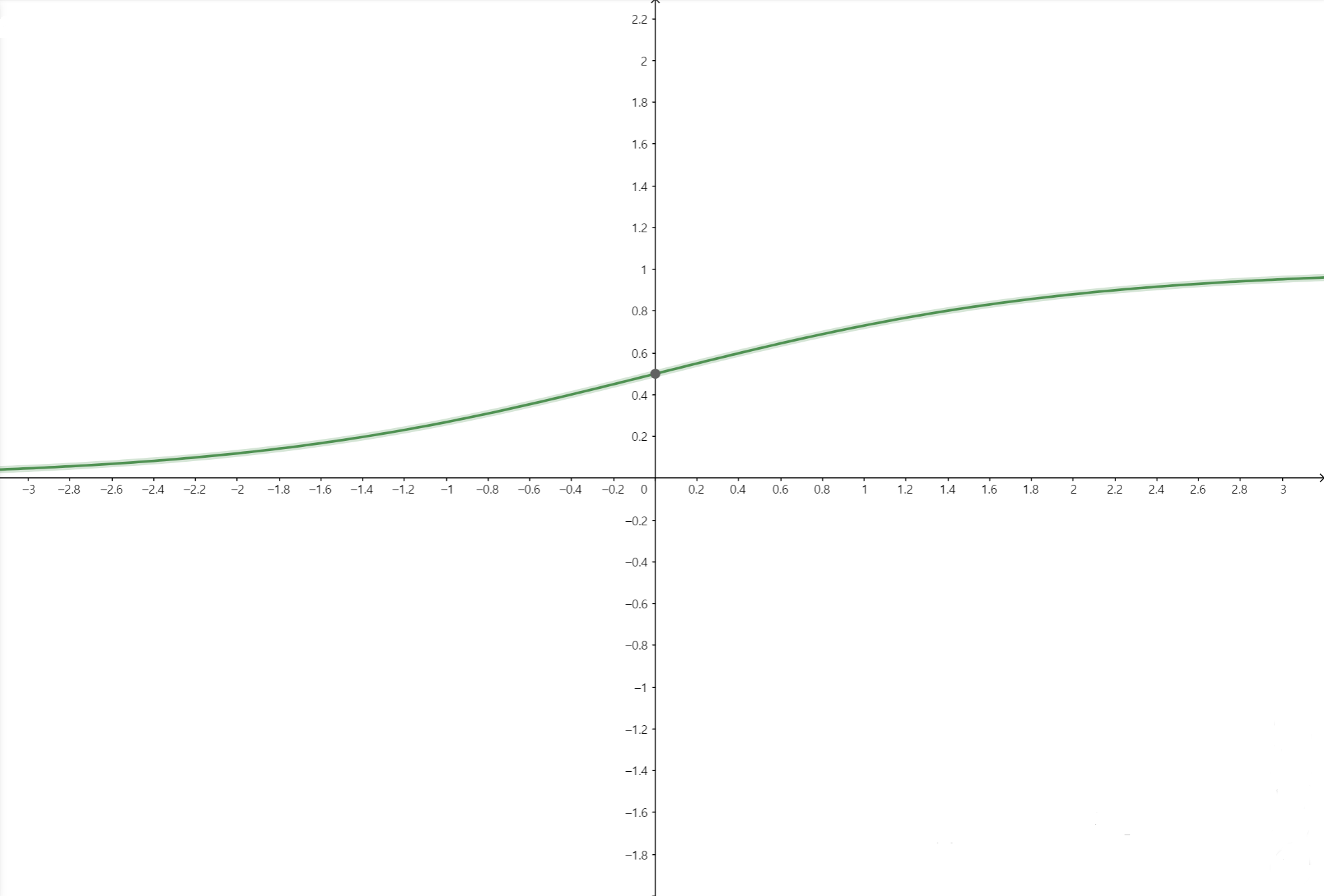
위의 $\beta_0+\beta_1x$ 식을 $x$가 $\mathbb R^{n_x}$에 속할 때에도 적용하기 위해, 벡터를 이용하여 정의하기 위해 weight vector $\boldsymbol w$와 bias $b$를 적용하면 다음과 같이 표현할 수 있습니다.

\[P(y=1 \mid \boldsymbol x) = \sigma(\boldsymbol w^T\boldsymbol x + b) = \frac{\exp(\boldsymbol w^T\boldsymbol x + b)}{1 + \exp(\boldsymbol w^T\boldsymbol x + b)}\]

모든 $y$가 가질 수 있는 outcome에 대해서 확률의 합은 1이 되어야 하므로

\[P(y =1 \mid \boldsymbol x) = 1-P(y=1 \mid \boldsymbol x) = \frac{1}{1+\exp(\boldsymbol w^T\boldsymbol x + b)}\]

가 됩니다.

(3) Cost function

위에서와 같이 $\boldsymbol x$가 주어졌을 때 $y=1$일 확률을

\[P(y=1 \mid \boldsymbol x) = \sigma(\boldsymbol w^T\boldsymbol x + b) = \frac{\exp(\boldsymbol w^T\boldsymbol x + b)}{1 + \exp(\boldsymbol w^T\boldsymbol x + b)}\]

다음과 같이 정의하였을 때, 우리의 목표는 $\boldsymbol w, b$를 찾는 것입니다. (이를 제외한 나머지 값은 다 알고 있기 때문입니다.) 그렇다면 어떤 $\boldsymbol w, b$를 찾아야 할까요. 주어진 데이터 $(\boldsymbol x^{(1)}, y^{(1)}), …, (\boldsymbol x^{(m)}, y^{(m)})$에 대해서 만약

\[y^{(i)} = 1\]

이라면,

\[P(y=1 \mid \boldsymbol x = \boldsymbol x^{(i)})\]

값이 커야 합니다. $y=1$이기 때문이죠. 반대로,

\[y^{(i)} = 0\]

이라면

\[P(y=0 \mid \boldsymbol x = \boldsymbol x^{(i)}) = 1- P(y=0 \mid \boldsymbol x = \boldsymbol x^{(i)})\]

의 값이 커야 합니다. 위 두식을 한번에 정의하는 방법은 다음과 같습니다.

\[P(y=j \mid \boldsymbol x = \boldsymbol x^{(i)}) = P(y=1 \mid x=\boldsymbol x^{(i)})^jP(y=0 \mid x= \boldsymbol x^{(i)})^{1-j}\]

만약 $j=1$이라면, $P(y=0 \mid x=\boldsymbol x^{(i)})$항이 사라지고, $j=0$이라면, $P(y=1 \mid x=\boldsymbol x^{(i)})$항이 사라집니다. 여기서

\(\hat{y}^{(i)} = \sigma(\boldsymbol w^T\boldsymbol x^{(i)} + b)\) 로 설정하면 위의 식에 logistic regression 모형을 적용하면

\[P(y=y^{(i)} \mid \boldsymbol x = \boldsymbol x^{(i)}) = (\hat{y}^{(i)})^{y^{(i)}}(1-\hat{y}^{(i)})^{1-y^{(i)}}\]

가 됩니다. 계산의 편의를 위해 양변에 log를 취하면

\[\log P(y=y^{(i)} \mid \boldsymbol x = \boldsymbol x ^{(i)}) =y^{(i)}\log(\hat{y}^{(i)})+(1-y^{(i)})\log(1-\hat{y}^{(i)})\]

가 됩니다. 해당 값이 클수록 실제 y값을 맞출 확률이 크다는 뜻이니, 위의 값이 커야 합니다. 여기서 계산상의 편의를 위해 양변에 -를 곱한

\[L(\hat{y}^{(i)}, y^{(i)}) = -\log P(y=y^{(i)} \mid \boldsymbol x = \boldsymbol x ^{(i)}) = -y^{(i)}\log(\hat{y}^{(i)})-(1-y^{(i)})\log(1-\hat{y}^{(i)})\]

값을 $i$번 째 observation에 대한 loss이고 이를 일반화한 \(L(\hat{y}, y )= -y\log(\hat{y})-(1-{y})\log(1-\hat{y})\)

다음 식을 logistic regression에서의 loss function이라고 합니다. Loss는 작을수록 실제 $y$값을 얻을 확률이 큽니다.

이러한 observation이 $m$개 있으므로, $m$개의 데이터에 대해 위의 값을 모두 더하고(더하는 이유를 알려면 likelihood와 log-likelihood에 대해 알아야 합니다. appendix 참고) 개수로 나눈

\[J(\boldsymbol w, b) =\frac{1}{m}\sum_{i=1}^mL(\hat{y}^{(i)}, y^{(i)})\]

를 Cost function이라고 합니다. 즉, 우리가 찾는 $\boldsymbol w, b $는 다음 cost function을 최소화시키는 값입니다.

우리가 구해야 하는 값과 최소화시켜야 하는 함수를 알게 되었으니, 다음은 어떤 방법으로 최소화를 시킬까입니다. 이 때 사용되는 방법이 Gradient descent입니다.

(4) Gradient Descent

위에서 계산상의 편의를 위해 log 함수를 붙이거나, -를 붙이는 작업을 하였습니다. 이러한 작업을 한 이유가 Gradient Descent를 간단히 적용하기 위해서인데요. Gradient Descent 방법을 적용하기 위해서는 convex 함수에 대해서 알아야 합니다.

Definition : Convex function

$f$ is called convex if and only if

For all $0\leq t < 1$ and all $x_1, x_2 \in X$,

\[f(tx_1 +(1-t)x_2) \leq tf(x_1) +(1-t)f(x_2)\]

다음 조건을 만족하는 함수를 convex function이라고 정의합니다. 2차원 평면에서 함수를 그렸을 때 아래로 볼록한 함수를 convex function으로 정의를 합니다.

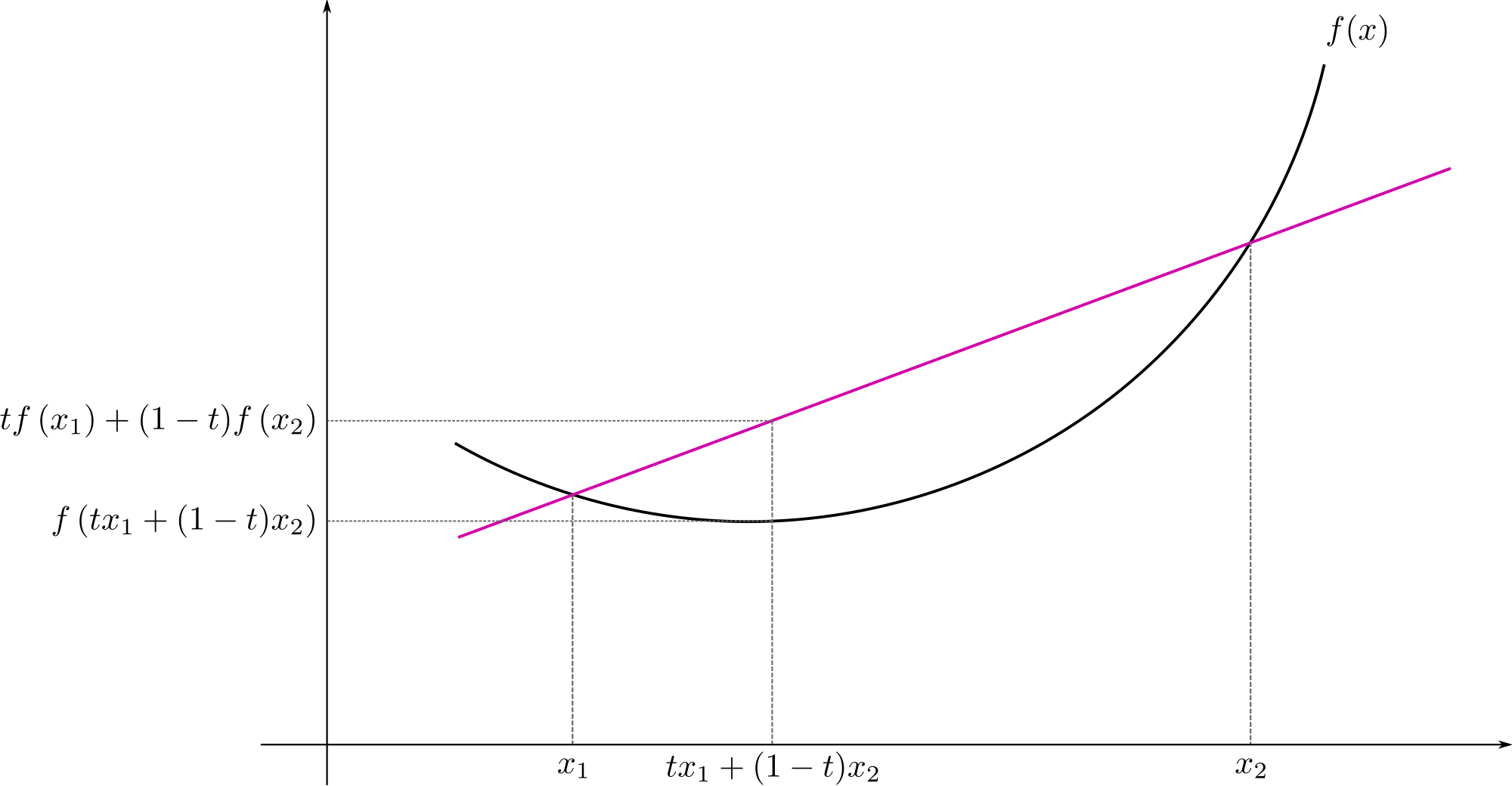
Monotone(감소하지 않는 함수 또는 증가하지 않는 함수)이 아닌 Convex function이 가지는 중요한 특징은 다음과 같습니다.

1. 최솟값이 하나로 존재한다.
2. 최댓값은 존재하지 않는다.

또한 만약 convex function이 충분히 smooth해서 미분이 충분히 가능하다면, convex function이 최소가 되는 지점은 그 지점에서 미분했을 때 0이 됩니다. 즉

\[f(c) : minimum \ of \ f(\cdot) \Rightarrow f'(c) =0\]

만약, $\boldsymbol x$가 벡터라면, $\boldsymbol x = \boldsymbol c$에서 $f$가 최솟값을 가지면, $\boldsymbol x = \boldsymbol c$에서의 gradient가 0이 됩니다.

\[f(\boldsymbol c) : minimum \ of \ f(\cdot) \Leftrightarrow gradient \ of \ f(\cdot) \ at \ \boldsymbol x = \boldsymbol c \ is \ 0\]

현재 우리가 구해야 하는 cost function

\[J(\boldsymbol w, b)\]

를 최소로 만드는 $\boldsymbol w, b$에서의 $J$의 gradient는 0이 됩니다.

하지만, 현재 $J(\boldsymbol w, b)$의 gradient를 구한다고 하더라도, $\boldsymbol w$의 차원에 따라 풀어야할 식이 많아지기 때문에, 실제로 정확한 값으로 나오지는 않습니다. 따라서 정확한 값을 구하는 대신 근사한 값으로 대체하는 방법인 gradient descent를 사용합니다.

Meaning of Gradient

Gradient의 의미를 확인하기 위해 다음 함수를 생각해봅시다.

\[f(x) = x^2\]

$f(x)$의 gradient인 derivative

\[f'(x) = 2x\]

입니다. $x=1$일 때의 값은

\[f'(1) = 2\]

입니다. 여기서, 중요한 점은 결과값의 부호를 살펴보시기 바랍니다.

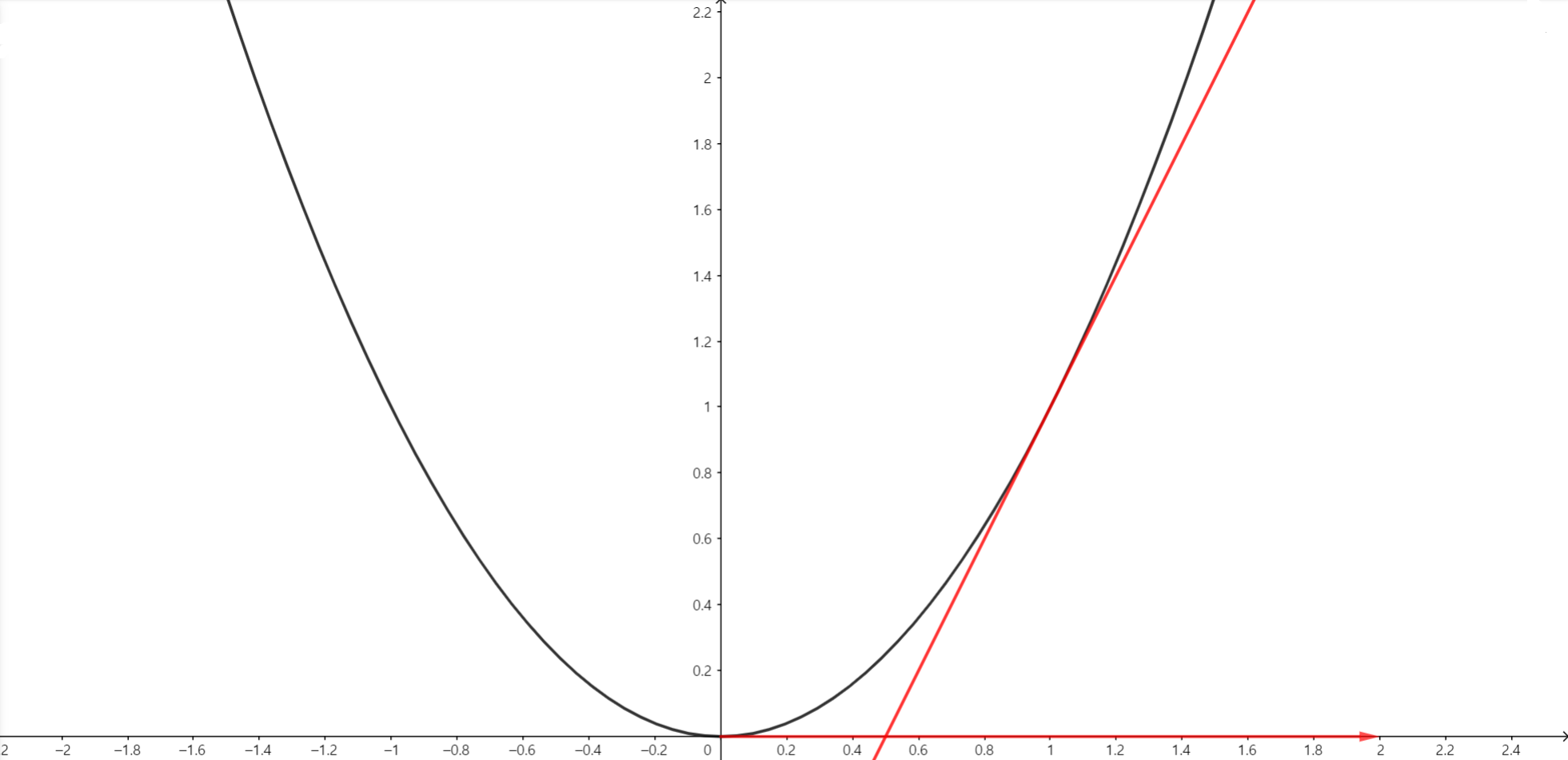
검은색 그래프가 $f(x) =x^2$, 빨간색 직선 그래프가 $x=1$에서의 $f(x)$의 접선인 $y=2x-1$, 마지막으로 x축에 표시된 벡터가 $(2, 0)$ 벡터입니다.

이 때 벡터의 $x$값만 살펴보면 $2$로, $x=1$에서의 gradient 값을 뜻합니다.

핵심은 방향입니다. $x$가 $f(x)$의 $x=1$에서의 gradient방향으로 증가하면 $f(x)$는 어떻게 되나요? 바로 증가하게 됩니다!

마찬가지로, $x=-1$에서의 gradient를 구하면 $-2$가 되는데, 이 방향으로 $x$를 변화시키면 $f(x)$는 증가하게 됩니다.

정리하면, Gradient 방향으로 $\boldsymbol x$값을 이동시켰을 때, $f(\boldsymbol x)$값이 가장 급격하게 증가합니다. 이를 뒤집어서 생각하면

• Gradient 반대 방향으로 $\boldsymbol x$값을 이동시켰을 때, $f(x)$값이 가장 급격하게 감소합니다.

이 원리를 이용하여 최솟값을 찾는 방법이 gradient descent 방법입니다.

Gradient Descent

Cost function $J(\boldsymbol w, b)$에 대해 gradient descent는 다음의 순으로 진행됩니다.

1. 초기값 $\boldsymbol w, b$를 설정합니다.
2. 반복적으로
   1. $\boldsymbol w, b$에서의 gradient를 구합니다. 해당 gradient를 $\frac{\partial J(\boldsymbol w,b)}{\partial\boldsymbol w}, \frac{\partial J(\boldsymbol w, b)}{\partial b}$라고 정의합니다.
   2. $\boldsymbol w := \boldsymbol w -\alpha \frac{\partial J(\boldsymbol w,b)}{\partial\boldsymbol w} $
   3. $b := b - \alpha \frac{\partial J(\boldsymbol w, b)}{\partial b}$
3. $\frac{\partial J(\boldsymbol w,b)}{\partial\boldsymbol w}, \frac{\partial J(\boldsymbol w, b)}{\partial b}$이 0에 가까워질 때까지, 또는 특정 횟수까지 2번을 반복합니다.

Gradient의 반대방향으로 이동시켰을 때 $J(\boldsymbol w, b)$값이 가장 급격하게 감소하기 때문에, 주어진 $\boldsymbol w, b$에서 gradient의 반대방향으로 조금씩 이동하여 최솟값을 찾는 방법이 Gradient descent 방법입니다.

지금까지 Logistic regression과 Cost function, Gradient descent에 대해 알아보았습니다. 다음 포스트에서는 이어서 computation graph을 통한 실제 gradient descent 계산 방법에 대해서 알아보도록 하겠습니다. 질문이나 오류 있으면 댓글 남겨주세요! 감사합니다!

Appendix : Maximum Likelihood Estimation

확률변수 $Y_1, …, Y_n$이 있고, 이들은 각각 독립적으로 다음과 같은 확률밀도함수를 가집니다.

\[Y_i \sim f_{Y_i}(y ; \theta)\]

$\theta$는 확률밀도함수를 구성하는 값(또는 모집단을 설명하는 값)으로 parameter(모수)라고 합니다. 만약 $\theta$의 값을 정확하게 알고 있다면, $Y_i$의 분포를 정확하게 알고 있으므로, $Y_i$에 대해 완벽하게 설명을 할 수 있습니다. 하지만 $\theta$를 모르기 때문에, 우리는 위의 밀도함수로부터 추출된 $Y_1, …, Y_n$인 $y_1, …, y_n$을 통하여 $\theta$를 추정하게 됩니다. 그렇다면 어떤 방식으로 추정을 하는 것일까요?

$f_{Y_i}(y;\theta)$는 $Y_i=y$일 때의 확률 값입니다. 그렇다면, 현재 주어진 observation $y_1, …, y_n$이 나올 확률은 다음과 같습니다.

\[P(Y_1 = y_1, ..., Y_n=y_n) = P(Y_1=y_1)\cdots P(Y_n=y_n) = f_{Y_1}(y_1;\theta)\cdots f_{Y_n}(y_n; \theta)\]

()$Y_i$들이 분리되는 이유는 $Y_i$끼리 독립이기 때문입니다.)

Maximum likelihood estimation은 다음과 같은 아이디어에서 출발합니다. 해당 observation이 나온 이유는 해당 observation이 나올 확률이 가장 크기 때문이다!

따라서 해당 확률 값을 parameter인 $\theta$의 입장($\theta$를 변수로 표현)에서 작성한 식인

\[L(\theta) = f_{Y_1}(y_1;\theta)\cdots f_{Y_n}(y_n;\theta)\]

를 likelihood라고 하며 해당 값을 최대로 만드는 $\theta$를 Maximum likelihood estimator(mle)라고 합니다. 또한 likelihood를 최대로 만드는 $\theta$를 estimator로 쓰는 방법을 maximum likelihood estimation이라고 합니다.

위에서 배운 logistic regression에서의 cost function은 사실 해당 likelihood 값에 -를 곱한 값입니다(convex 함수로 만들기 위해서죠.). 따라서 logistic regression에서 cost function을 이용하여 구한 $\boldsymbol w, b$값은 maximum likelihood estimation 방법을 이용하여 구한 mle입니다.