1.3 Vector Equation

세 번째 포스트에서는 linear system을 표현하는 방법 중 하나인 vector equation와 이와 관련된 중요한 개념인 linear combination, spanning set에 대해서 다루어 보겠습니다.

(이번 포스트에서 vector와 scalar에 대한 내용이 나오는데, 내용이 너무 방대하여서 고등학교에서 배우는 벡터의 개념과 벡터를 순서쌍으로 해석하는데 도움이 되는 위치 벡터, 벡터 연산에 대한 내용만을 다루겠습니다. )

1) Vector and Scalar

scalar는 크기만을 가지는 값을 뜻하고, vector는 크기와 방향을 모두 가지는 값을 뜻합니다. 고등학교에서 배우는 벡터를 보면 화살표를 이용하여 나타냅니다. (화살표의 길이로 크기를, 화살표 방향으로 방향을 나타낼 수 있기 때문입니다.)

여기서, 벡터의 시작지점을(화살표 시작지점) 시점, 벡터가 끝나는 지점(화살표 끝 지점)을 종점이라고 하고, 벡터의 길이를 벡터의 크기라고 합니다.

벡터에 대한 중요한 점 중 하나는 벡터를 정의할 때는 크기와 방향만 정의하지, 벡터의 위치에 대해서는 정의하지 않습니다. 즉 크기와 방향이 같은 벡터는 어느 위치에 놓여 있든 같은 벡터라고 정의합니다.

$\boldsymbol{v}$의 시점은 $A$, 종점은 $B$, $\boldsymbol{u}$의 시점은 $C$ 종점은 $D$입니다. 두 벡터의 위치는 달라도, 방향과 크기가 같기 때문에($\boldsymbol{u}$를 평행이동시키면 $\boldsymbol{v}$와 일치합니다.) 두 벡터는 같습니다.

(1) 위치 벡터

벡터가 있는 위치가 다르더라도, 크기와 방향이 같다면 두 벡터는 같은 벡터로 정의합니다.

그래서, 벡터의 시점을 원점 $O$로 고정시키는 순간, 각각의 벡터는 점 하나와 일대일 대응이 됩니다. (종점과 일대일 대응입니다.)

따라서 만약 $\mathbb{R}^2$에서의 모든 벡터의 시점을 원점 $O$로 고정시키면, 각각의 벡터를 좌표 순서쌍으로 나타낼 수 있습니다.

이를 확장을 하면, $\mathbb{R}^2$가 아닌 $\mathbb{R}^3$, $\mathbb{R}^4$, …, $\mathbb{R}^n$에서의 모든 벡터의 시점을 원점으로 고정시켜, 각각의 벡터를 좌표 순서쌍으로 나타낼 수 있습니다.

따라서 벡터를 순서쌍으로 정의를 할 수 있습니다.

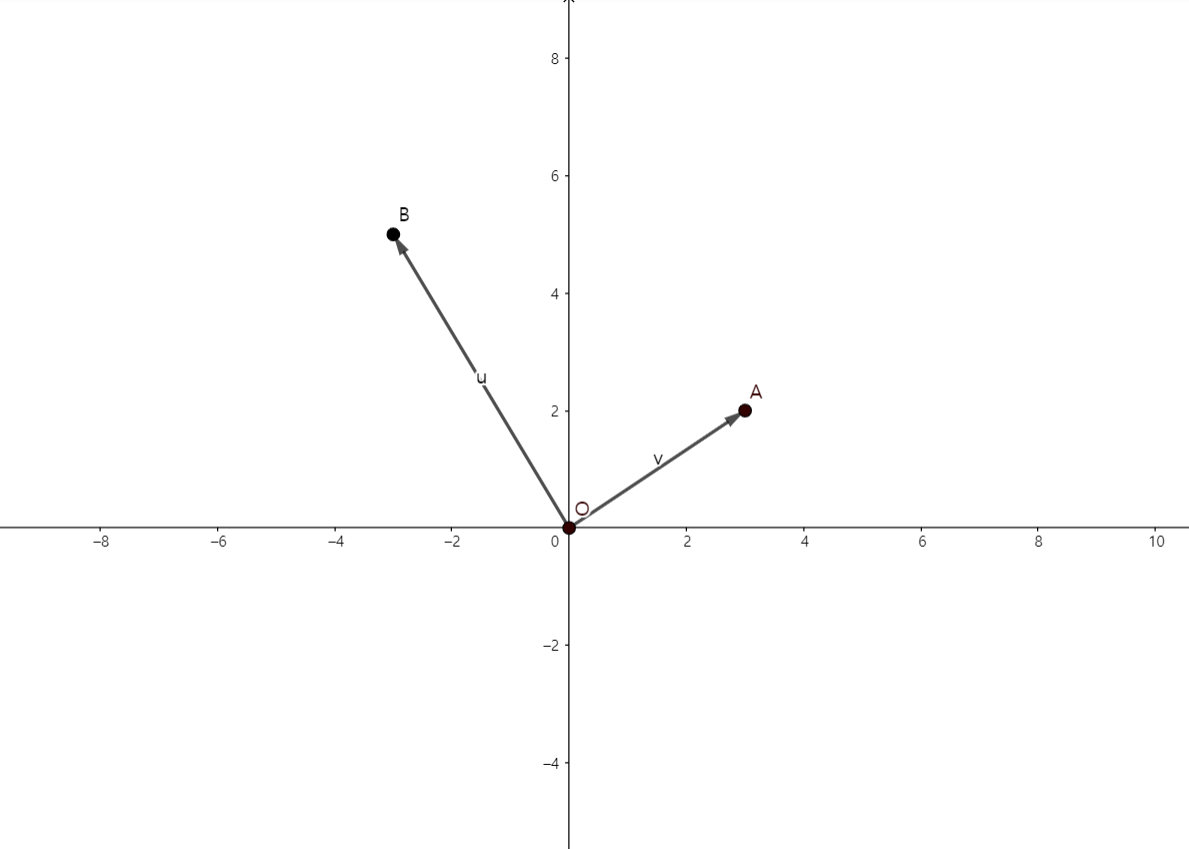
(시점을 원점으로 고정시키는 순간 벡터와 점은 일대일 대응이 됩니다.(벡터와 종점이 대응됩니다.) 따라서 벡터를 좌표 순서쌍으로 나타낼 수 있습니다.)

(2) Zero Vector, $\mathbb{R}^n$ 정의

• Definition

n개의 실수로 이루어진 순서쌍 $(v_1, v_2, …, v_n)$을 모두 모아놓은 집합

\[\{ \boldsymbol{v} \ |\ v_1, v_2, ..., v_n \in \mathbb{R} \}\]

를 n-space라고 정의하고, $\mathbb{R}^n$으로 표시합니다.

• Definition

$\mathbb{R}^n$에서 모든 성분값이 0인 벡터 \((0, 0, ... ,0)\) 을 zero vector, 또는 origin of $\mathbb{R}^n$이라고 합니다.

(3) Notation

vector를 다음의 방법으로 표시할 수 있습니다.

\[\boldsymbol{v}= (v_1, v_2, ..., v_n)\] \[\boldsymbol{v} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix}\] \[\boldsymbol{v} = [v_1 , v_2, \cdots , v_n]\]

특히 두 번째 표시방법은 많이 사용이 되니 한번 더 확인을 해주면 되겠습니다.

(4) Vector의 상등, 연산

• Definition

두 벡터 $\boldsymbol{v} = (v_1, v_2, …, v_n)$와 $\boldsymbol{w}=(w_1, w_2, …, w_n)$가

\[v_1=w_1,\ v_2=w_2, \cdots , v_n=w_n\]

의 조건을 만족하면, 두 벡터가 같다(equivalent)라고 정의하고, $\boldsymbol{v}=\boldsymbol{w}$로 표시합니다.

• Definition

$\mathbb{R}^n$에 있는 두 벡터 $\boldsymbol{v} = (v_1, v_2, …, v_n)$와 $\boldsymbol{w}=(w_1, w_2, …, w_n)$와 scalar $k$에 대해서

• $\boldsymbol{v}+\boldsymbol{w}=(v_1+w_1, \ v_2+w_2, \ \cdots , v_n+w_n)$
• $k\boldsymbol{v}=(kv_1, \ kv_2, \ , \cdots, kv_n)$
• $-\boldsymbol{v}=(-v_1, \ -v_2, \ \cdots , -v_n)$
• $\boldsymbol{v}-\boldsymbol{w}=(v_1-w_1, \ v_2-w_2, \ \cdots , v_n-w_n)$

로 벡터의 덧셈, 뺄셈, scalar배를 정의합니다.

2) Linear Combination

위 내용까지가 기본적인 벡터에 대한 내용이었다면, 이제 linear system과 vector를 연결시키는 작업을 해보겠습니다. 이 작업을 하기 위해서, linear combination이라는 중요한 개념을 사용합니다.

• Definition: Linear combination of $\boldsymbol{v_1}, \boldsymbol{v_2}, \cdots, \boldsymbol{v_p} $

Given vectors $\boldsymbol{v_1}, \boldsymbol{v_2}, \cdots, \boldsymbol{v_p} $ in $\mathbb{R}^n$ and given $c_1, c_2, \cdots, c_p$(scalar), the vector $\boldsymbol{y}$ defined by

\[\boldsymbol{y} = c_1\boldsymbol{v_1}+c_2\boldsymbol{v_2}+\cdots+c_p\boldsymbol{v_p}\]

is called a linear combination of $\boldsymbol{v_1}, \boldsymbol{v_2}, \cdots, \boldsymbol{v_p} $ with weights $c_1, c_2, \cdots, c_p$

위 정의를 정리하면, $\boldsymbol{v_1}, \boldsymbol{v_2}, \cdots, \boldsymbol{v_p} $ 일차 결합으로 나타내어진 $\boldsymbol{y}$를 $\boldsymbol{v_1}, \boldsymbol{v_2}, \cdots, \boldsymbol{v_p} $ 의 linear combination이라고 합니다.

Example

\[\boldsymbol{a_1}=\begin{bmatrix} 1 \\-2\\-5 \end{bmatrix}, \ \boldsymbol{a_2}=\begin{bmatrix} 2 \\5\\6 \end{bmatrix}, \ \boldsymbol{b}=\begin{bmatrix} 7 \\4\\-3 \end{bmatrix}\]

다음의 세 벡터가 있습니다. 여기서, $\boldsymbol{b}$ 는 $\boldsymbol{a_1}, \boldsymbol{a_2}$에 의해 다음과 같이 나타낼 수 있습니다.

\[\boldsymbol{b} = 3\boldsymbol{a_1} + 2\boldsymbol{a_2}\]

이 때 $\boldsymbol{b}$ 는 $\boldsymbol{a_1}$, $\boldsymbol{a_2}$의 linear combination이고, weight는 $3, 2$입니다.

3) Vector Equation

Linear combination과 linear system의 관계를 살펴봅시다.

example에서 $\boldsymbol{b}$ 가 $\boldsymbol{a_1}$, $\boldsymbol{a_2}$ 의 linear combination인지 아닌지 모르는 상황이라고 가정해봅시다.

$\boldsymbol{b}$ 가 $\boldsymbol{a_1}$, $\boldsymbol{a_2}$의 linear combination인지 아닌지 확인하는 것은

\(\boldsymbol{b} = c_1\boldsymbol{a_1} + c_2\boldsymbol{a_2}\) 를 만족하는 $c_1, c_2$가 존재하는지 아닌지 확인을 하는 것과 같습니다.

위 식을 풀어서 적으면

\[\begin{bmatrix} 7 \\4\\-3 \end{bmatrix} = c_1\begin{bmatrix} 1 \\-2\\-5 \end{bmatrix} + c_2\begin{bmatrix} 2 \\5\\6 \end{bmatrix}\]

가 되어, 위 식을 $c_1, c_2$에 대한 linear system으로 나타낼 수 있습니다.

\[\begin{aligned} c_1+2c_2&=7 \\ -2c_1+5c_2&=4 \\ -5c_1+6c_2&=-3 \end{aligned}\]

즉, $\boldsymbol{b}$ 가 $\boldsymbol{a_1}$, $\boldsymbol{a_2}$의 linear combination인지 아닌지 확인하는 것은 다음의 linear system이 consistent한지 아닌지 확인하는 작업과 같습니다.

위 linear system을 풀었을 때, $c_1=3, c_2=2$가 나와,

\[\boldsymbol{b} = 3\boldsymbol{a_1} + 2\boldsymbol{a_2}\]

으로 표현할 수 있습니다.

위의 example을 정리하면, linear system을 vector와 linear combination을 이용하여 표현할 수 있습니다.

Vector Equation은 다음과 같이 표현할 수 있습니다.

$\boldsymbol{a_1}, \boldsymbol{a_2}, \cdots, \boldsymbol{a_p} , \boldsymbol{b} \in \mathbb{R}^n $, $x_1, x_2, …, x_n \in \mathbb{R}$,

\[x_1\boldsymbol{a_1}+x_2\boldsymbol{a_2}+\cdots+x_p\boldsymbol{a_p}=\boldsymbol{b}\]

여기서, $\boldsymbol{a_1}, \boldsymbol{a_2}, \cdots, \boldsymbol{a_p} , \boldsymbol{b} \in \mathbb{R}^n $ 은 fixed된 값이고, 변수는 $x_1, x_2, …, x_n \in \mathbb{R}$입니다.

위 vector equation의 solution을 찾는 것은, 다음의 augmented matrix

\[\begin{bmatrix} \boldsymbol{a_1} & \boldsymbol{a_2} & ... & \boldsymbol{a_p} & \boldsymbol{b} \end{bmatrix}\]

를 가지는 linear system의 solution을 찾는 것과 일치합니다.

만약 위 linear system이 solution을 가지면, 위의 vector equation의 solution 또한 존재하고, 이는 $\boldsymbol{b}$는 $\boldsymbol{a_1}, \boldsymbol{a_2}, …, \boldsymbol{a_p}$의 linear combination인 것을 의미합니다.

위 linear system이 solution을 가지지 않으면(inconsistent하면), 위의 vector equation의 solution 또한 존재하지 않고, 이는 $\boldsymbol{b}$는 $\boldsymbol{a_1}, \boldsymbol{a_2}, …, \boldsymbol{a_p}$의 linear combination이 아닌 것을 의미합니다.

4) Spanning Set

Linear combination을 이용한 특별한 집합인 spanning set에 대해서 알아보겠습니다.

• Definition: Spanning Set

If $\boldsymbol{v_1}, \boldsymbol{v_2}, …, \boldsymbol{v_p}$ are in $\mathbb{R}^n$, then the set of all linear combinations of $\boldsymbol{v_1}, \boldsymbol{v_2}, …, \boldsymbol{v_p}$ is denoted by $Span { \boldsymbol{v_1}, \boldsymbol{v_2}, …, \boldsymbol{v_p} }$

is called the subset of $\mathbb{R}^n$ spanned by $\boldsymbol{v_1}, \boldsymbol{v_2}, …, \boldsymbol{v_p}$

정리하면, $\boldsymbol{v_1}, \boldsymbol{v_2}, …, \boldsymbol{v_p}$의 모든 linear combination을 모은 집합이 $Span { \boldsymbol{v_1}, \boldsymbol{v_2}, …, \boldsymbol{v_p} }$이 되고, 수식으로 표현하면

\[Span \{ \boldsymbol{v_1}, \boldsymbol{v_2}, ..., \boldsymbol{v_p} \} = \{\boldsymbol{y} | \boldsymbol{y} = c_1\boldsymbol{v_1}+c_2\boldsymbol{v_2}+\cdots+c_p\boldsymbol{v_p}, \ \ c_1, c_2, ..., c_p \in \mathbb{R}^n \}\]

여기서, $\boldsymbol{b}$​이 $Span { \boldsymbol{v_1}, \boldsymbol{v_2}, …, \boldsymbol{v_p} }$에 포함되는지 안되는지 확인하는 것은

$\boldsymbol{b}$가 $\boldsymbol{v_1}, \boldsymbol{v_2}, …, \boldsymbol{v_p}$의 linear combination인지 아닌지 확인하는 것과 같고, 이를 확인하는 것은

\[x_1\boldsymbol{v_1}+x_2\boldsymbol{v_2}+\cdots+x_p\boldsymbol{v_p}=\boldsymbol{b}\]

의 vector equation을 풀어서 solution이 있는지 없는지 확인하는 것과 같습니다.

5) Parametric vector form

이 때까지 linear system을 vector equation으로 표현하는 방법과, linear combination과 spanning set에 대해서 알아보았습니다. 이번에는 linear system의 solution을 vector form으로 표현하는 방법에 대해서 알아보겠습니다.

example

\[10x_1-3x_2-2x_3=0\]

다음의 linear system의 augmented matrix는

\[\begin{bmatrix} 10 & -3 &-2 &0 \end{bmatrix}\]

입니다. 이 matrix를 reduced echelon form은

\[\begin{bmatrix} 1 & \frac{-3}{10} &-\frac{2}{10} &0 \end{bmatrix}\]

이 됩니다. 이를 linear system으로 나타내면

\[x_1-\frac{3}{10}x_2-\frac{2}{10}x_3=0 \\ x_1=\frac{3}{10}x_2+\frac{2}{10}x_3\]

이 됩니다. linear system의 solution $x_1, x_2, x_3$를 vector $\boldsymbol{x}$로 나타내면

\[\boldsymbol{x}=\begin{bmatrix} \frac{3}{10}x_2 + \frac{2}{10}x_3 \\x_2 \\x_3 \end{bmatrix} = x_2 \begin{bmatrix}\frac{3}{10} \\ 1 \\ 0\end{bmatrix} + x_3\begin{bmatrix}\frac{2}{10} \\ 0 \\ 1\end{bmatrix} \\ x_2, x_3 : free\ variable\]

와 같이 vector form으로 표현할 수 있습니다.

example

\[\begin{aligned} 3x_1+5x_2-4x_3&=0\\ -3x_1-2x_2+4x_3&=0\\ 6x_1+x_2-8x_3&=0 \end{aligned}\]

다음 linear system의 augmented matrix는

\[\begin{bmatrix} 3 & 5 & -4 & 0 \\ -3 & -2 & 4 & 0 \\ 6 & 1 & -8 & 0 \end{bmatrix}\]

이 됩니다. 위 agumented matrix를 row operation을 통하여 reduced echelon form으로 만들어주면

\[\begin{bmatrix} 3 & 5 & -4 & 0 \\ -3 & -2 & 4 & 0 \\ 6 & 1 & -8 & 0 \end{bmatrix} \sim \begin{bmatrix} 3 & 5 & -4 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & -9 & 0 & 0 \end{bmatrix} \sim \begin{bmatrix} 3 & 0 & -4 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \sim \begin{bmatrix} 1 & 0 & -\frac{4}{3} & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}\]

와 같이 나타낼 수 있고, 이를 정리하면

\[x_1= \frac{4}{3}x_3\\ x_2=0\\ x_3 : free \ variable\]

과 같이 나타낼 수 있습니다. 이를 vector $\boldsymbol{x}$로 나타내면

\[\boldsymbol{x} = x_3\begin{bmatrix}\frac{4}{3} \\ 0 \\ 1\end{bmatrix} \\ x_3 : free\ variable\]

로 나타낼 수 있습니다.

지금까지 linear system과 vector equation, linear combination과 spanning set에 대해서 알아보았습니다. 다음 포스트에서는 linear system을 표현하는 방법 중 matrix를 이용하여 표현하는 방법에 대해서 알아보겠습니다.