6.3 Orthogonal Projection
이번 포스트에서는 orthogonal projection에 대해 알아보겠습니다.
1) Orthogonal Projection
(1) Orthogonal projection
Orthogonal projection의 목표는 다음과 같습니다.
$\mathbb R^n$의 subspace $W$와 벡터 $\boldsymbol y$에 대해서 $W$에 속하는 벡터 중 다음 조건을 만족하는 벡터 $\hat {\boldsymbol y}$을 찾고 싶습니다.
- $\boldsymbol{y}-\hat{\boldsymbol{y}}$가 $W$에 orthogonal합니다.
- $\boldsymbol y$에서 $W$에 가장 가까운 벡터가 $\hat{\boldsymbol{y}}$입니다.
해당 상황을 시각적으로 표현하면 다음과 같습니다.
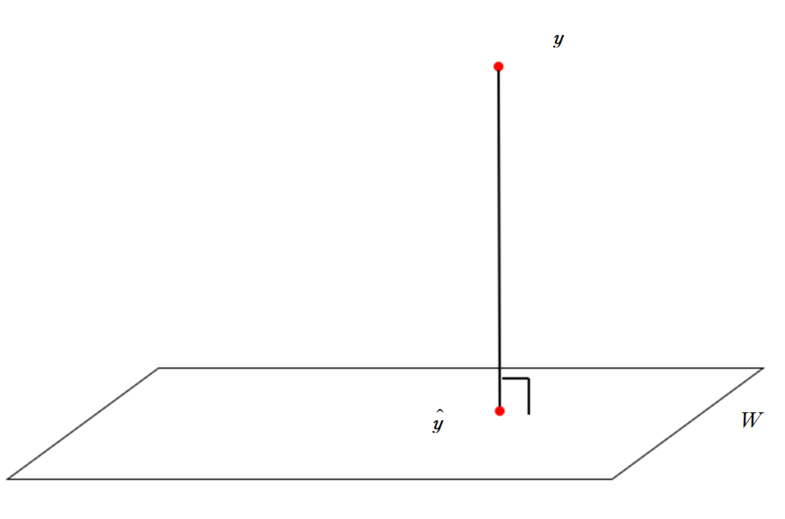
이러한 $\hat{\boldsymbol{y}}$는 unique하게 존재하는데, 왜 unique하게 존재하는지, 어떻게 해당 벡터를 찾을 수 있는지 알아보겠습니다.
${\boldsymbol{u_1}, …, \boldsymbol{u_n}}$이 $\mathbb R^n$의 orthogonal basis면, $\boldsymbol y \in \mathbb R^n$은
\[\boldsymbol{y} = \boldsymbol{z_1} + \boldsymbol{z_2}\]로 표현이 가능합니다. 여기서, $\boldsymbol{z_1}$은 basis에 속한 몇 개의 벡터의 linear combination으로 표현되는 벡터이고, $\boldsymbol{z_2}$는 basis에 속한 벡터 중 $\boldsymbol{z_1}$에 포함된 벡터를 제외한 나머지 벡터들의 linear combination으로 표현되는 벡터입니다.
이 때, $\boldsymbol{z_1}$과 $\boldsymbol{z_2}$는 orthogonal합니다. 예를 들어
\[\boldsymbol{z_1} = c_1\boldsymbol{u_1}+\cdots+c_k\boldsymbol{u_k}\\ \boldsymbol{z_2} = c_{k+1}\boldsymbol{u_{k+1}} + \cdots + c_n\boldsymbol{u_n}\]일 경우,
\[\boldsymbol{z_1} \perp \boldsymbol{z_2}\]가 됩니다. 또한 $\boldsymbol{z_1}$을 표현할 때 사용한 벡터 ${\boldsymbol{u_1}, …, \boldsymbol{u_k}}$를 basis로 하는 subspace $W$를 생각한다면, $\boldsymbol{z_1}\in W$을 만족합니다. 이 때, ${\boldsymbol{u_1}, …, \boldsymbol{u_n}}$이 orthogonal basis이므로,
\[\boldsymbol{z_2} \in W^\perp\]를 만족합니다. 또한, $\boldsymbol{z_2}$을 표현할 때 사용한 벡터 ${\boldsymbol{u_{k+1}, …, \boldsymbol{u_{n}}}}$을 basis로 하는 subspace는 바로 $W^\perp$입니다.
이 성질을 이용하면 orthogonal projection의 목적에 부합하는 $\hat{\boldsymbol y}$를 찾을 수 있습니다.
Theorem
Let $W$ be a subspace of $\mathbb R^n$. Then each $\boldsymbol{y}$ in $\mathbb R^n$ can be written uniquely in the form
\[\boldsymbol{y} =\hat{\boldsymbol{y}} +\boldsymbol{z}\]where $\hat{\boldsymbol{y}} \in W$ and $\boldsymbol z \in W^\perp$.
In fact, if ${\boldsymbol{u_1}, …, \boldsymbol{u_p}}$ is any orthogonal basis for $W$, then
\[\hat{\boldsymbol y} = \frac{\boldsymbol{u_1}\cdot \boldsymbol{y}}{\boldsymbol{u_1}\cdot \boldsymbol{u_1}}\boldsymbol{u_1} + \frac{\boldsymbol{u_2}\cdot \boldsymbol{y}}{\boldsymbol{u_2}\cdot \boldsymbol{u_2}}\boldsymbol{u_2} + \cdots + \frac{\boldsymbol{u_p}\cdot \boldsymbol{y}}{\boldsymbol{u_p}\cdot \boldsymbol{u_p}}\boldsymbol{u_p}\]and
\[\boldsymbol z = \boldsymbol y - \hat{\boldsymbol y}\]$\hat {\boldsymbol y}$ is called the orthogonal projection of $\boldsymbol y$ onto $W$
\[\hat{\boldsymbol y} = proj_{W}\boldsymbol y\]이전 포스트에서 orthogonal basis를 알고 있다면, 해당 subspace에 있는 벡터를 orthogonal basis의 linear combination으로 표현할 수 있는 방법을 배웠습니다. 그 방법이 위 정리에 적용이 되었습니다. 또한, 앞서 말한 특정 subspace와 subspace의 orthogonal complement에 속한 두 개의 벡터로 쪼갤 수 있는 성질을 이용하여 위 정리를 나타낼 수 있습니다. 특히, $\boldsymbol{y}$를 $W$에 속한 벡터와 $W^\perp$에 속한 벡터로 나타내었을 때, $W$에 속한 벡터인 $\hat{\boldsymbol y}$를 orthogonal projection of $\boldsymbol y$ onto $W$라고 합니다.
example
Let ${\boldsymbol{u_1}, …, \boldsymbol{u_5}}$ be an orthogonal basis for $\mathbb R^5$ and let
\[\boldsymbol{y} = c_1\boldsymbol{u_1}+\cdots c_5\boldsymbol{u_5}\]Consider the subspace $W=Span{\boldsymbol{u_1}, \boldsymbol{u_2}}$
$\boldsymbol{u_1}, \boldsymbol{u_2}$가 orthogonal하기 때문에, $W$의 basis는 ${\boldsymbol{u_1}, \boldsymbol{u_2}}$입니다.
$\boldsymbol{y}$ 벡터는 두 개의 벡터로 쪼개질 수 있습니다.
\[\boldsymbol{y}=\hat{\boldsymbol{y}} + \boldsymbol{z} \\ \hat{\boldsymbol{y}} =c_1\boldsymbol{u_1}+c_2\boldsymbol{u_2} \\ \boldsymbol{z} = c_3\boldsymbol{u_3}+c_4\boldsymbol{u_4}+c_5\boldsymbol{u_5}\]이 때, $\hat{\boldsymbol{y}} \in W$이고, $\boldsymbol{z} \in W^\perp$을 만족합니다. 따라서 $\hat{\boldsymbol{y}} = proj_W\boldsymbol{y}$ 가 됩니다.
example
\[\boldsymbol{u_1} = \begin{bmatrix} 2 \\ 5 \\ -1 \end{bmatrix}, \boldsymbol{u_2} = \begin{bmatrix}-2 \\ 1 \\ 1 \end{bmatrix}, \boldsymbol{y}=\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}, W=Span\{\boldsymbol{u_1}, \boldsymbol{u_2}\}\]$proj_W \boldsymbol y$를 구해봅시다. 먼저
\[\boldsymbol{u_1}\cdot \boldsymbol{u_2} = 0\]이므로 ${\boldsymbol{u_1}, \boldsymbol{u_2}}$는 $W$의 orthogonal basis입니다.
\[\boldsymbol{u_1}\cdot \boldsymbol{y} = 9, \ \ \boldsymbol{u_2}\cdot \boldsymbol{y} = 3 , \ \ \boldsymbol{u_1}\cdot\boldsymbol{u_1} =30, \ \ \boldsymbol{u_2} \cdot \boldsymbol{u_2} = 6\]을 이용하면 \(\frac{\boldsymbol{u_1}\cdot\boldsymbol{y}}{\boldsymbol{u_1}\cdot\boldsymbol{u_1}}=\frac{3}{10}, \ \ \frac{\boldsymbol{u_2}\cdot \boldsymbol{y}}{\boldsymbol{u_2}\cdot \boldsymbol{u_2}} = \frac{1}{2}\)
이므로
\[proj_W\boldsymbol y = \frac{3}{10}\boldsymbol u_1 + \frac{1}{2}\boldsymbol{u_2}\]임을 알 수 있습니다.
(2) Properties of orthogonal projection
orthogonal projection과 projection vector에 대한 다양한 성질에 대해 알아보도록 하겠습니다.
Theorem
Let ${\boldsymbol{u_1}, …, \boldsymbol{u_p}}$ be an orthogonal basis for a subspace $W$ of $\mathbb R^n$. For each $\boldsymbol{y}$ in $W$, the weights in the linear combination
\[\boldsymbol{y}=c_1\boldsymbol{u_1}+\cdots + c_p\boldsymbol{u_p}\]where $c_i = \frac{\boldsymbol{u_i}\cdot \boldsymbol{y} }{\boldsymbol{u_i} \cdot \boldsymbol{u_i}}\boldsymbol{u_i}$
In this case $proj_W \boldsymbol{y} = \boldsymbol{y}$
Projection의 목적이 $W$ 밖에 있는 벡터를 $W$에 존재하는 벡터와 $W^\perp$에 존재하는 벡터로 분리하여 표현하는 것이 목적입니다. 따라서, 만약 $\boldsymbol{y} \in W$이면, $\boldsymbol{y}$는 $W$의 orthogonal basis 벡터로 표현이 가능합니다.
\[\boldsymbol{y} = \hat{\boldsymbol{y}}+\boldsymbol{z}\]로 표현하였을 때, $\boldsymbol{z}=0 \in W^\perp$가 되는 것이구요.
Theorem : The best approximation theorem
Let $W$ be a subspace of $\mathbb R^n$, let $\boldsymbol{y}$ be any vector in $\mathbb R^n$, and let $\hat{\boldsymbol{y}}$ be the orthogonal projection of $\boldsymbol{y}$ onto $W$. Then $\hat{\boldsymbol{y}}$ is the closest point in $W$ to $\boldsymbol{y}$, in the sense that
\[\|\boldsymbol{y}-\hat{\boldsymbol{y}}\|<\|\boldsymbol{y}-\boldsymbol{v}\|\]for all $\boldsymbol{v}$ in $W$ distinct from $\hat{\boldsymbol{y}}$
위 정리를 통해서, $\boldsymbol{y}$의 $W$로의 orthogonal projection $\hat{\boldsymbol{y}}$가 $W$에 존재하는 벡터 중에 가장 $\boldsymbol{y}$와 가까운 것을 알 수 있습니다. 이를 시각적으로 나타내면 다음과 같습니다.
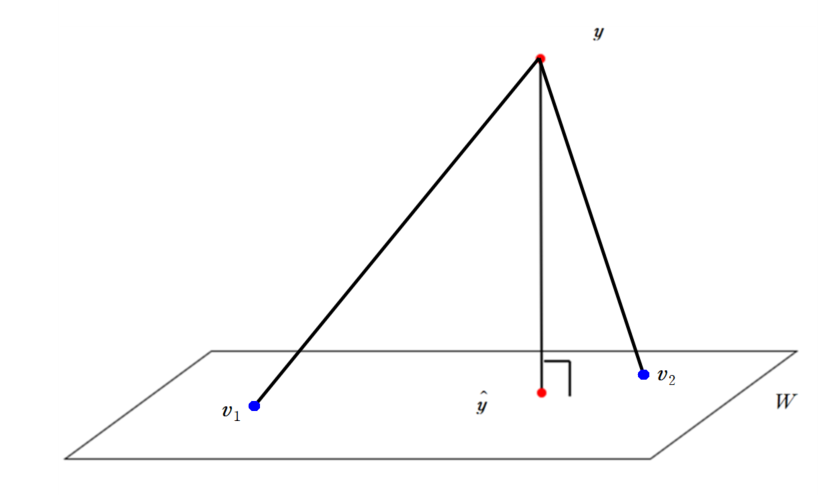
$\boldsymbol{y}$를 $W$에 projection시킨 벡터 $\hat{\boldsymbol{y}}$가 $W$에 속한 다른 벡터 $\boldsymbol{v_1}, \boldsymbol{v_2}$보다 가까운 것을 알 수 있습니다.
Caution and notation
orthogonal projection 벡터는 해당 벡터에서 subspace $W$에 가장 가까운 벡터임을 알 수 있었습니다. 즉, $W$에 있는 벡터 중에서 가장 $\boldsymbol{y}$와 비슷한 벡터가 $\hat{\boldsymbol{y}}$입니다. 따라서
\[\hat{\boldsymbol{y}} = proj_W \boldsymbol{y}\]를 the best approximation to $\boldsymbol{y}$ by elements of $W$라고 표현합니다. 또한 the best approximation theorem에서 사용한
\[\|\boldsymbol{y}-\boldsymbol{v}\|\]지표를 error of using $\boldsymbol{v}$ in place of $\boldsymbol{y}$라고 합니다. 이 때, 이 error는 $\boldsymbol{v}=\hat{\boldsymbol{y}}$일 때 최소화됩니다.
또한, $\hat{\boldsymbol{y}}$는 orthogonal basis에 의존하지 않습니다. 즉, 어떤 subspace $W$에 존재하는 orthogonal basis는 수없이 많을 수 있습니다. 하지만 $\hat{\boldsymbol{y}}$는 orthogonal basis와 상관없이 고정이되며, orthogonal basis가 바뀌었을 때 해당 orthogonal basis를 이용하여 $\hat{\boldsymbol{y}}$를 표현하는 방법(coefficient)만 달라집니다.
Theorem
If ${\boldsymbol{u_1}, …, \boldsymbol{u_p}}$ is an orthonormal basis for a subspace $W$ of $\mathbb R^n$, then
\[\hat{\boldsymbol{y}} = (\boldsymbol{u_1}\cdot \boldsymbol{y})\boldsymbol{u_1} + \cdots + (\boldsymbol{u_p}\cdot \boldsymbol{y})\boldsymbol{u_p}\]If $U=\begin{bmatrix} \boldsymbol{u_1} & … & \boldsymbol{u_p} \end{bmatrix}$,
\[proj_W\boldsymbol{y} = U^TU\boldsymbol{y}\]for all $\boldsymbol{y}\in\mathbb R^n$
orthonormal basis인 경우에는 basis에 속한 벡터의 length가 1이기 때문에, $\hat{\boldsymbol{y}}$를 계산할 때 각 coefficient부분의 분모부분을 계산하지 않아도 됩니다. 또한, 위 식을 matrix를 이용하여 표현 또한 가능합니다.
지금까지 orthogonal projection에 대해 알아보았습니다. 다음 포스트에서는 Gram-Schmidt Process에 대해 알아보겠습니다. 질문이나 오류 있으면 댓글 남겨주세요! 감사합니다!
Appendix : Proof of Theorem
Theorem
Let $W$ be a subspace of $\mathbb R^n$. Then each $\boldsymbol{y}$ in $\mathbb R^n$ can be written uniquely in the form
\[\boldsymbol{y} =\hat{\boldsymbol{y}} +\boldsymbol{z}\]where $\hat{\boldsymbol{y}} \in W$ and $\boldsymbol z \in W^\perp$.
In fact, if ${\boldsymbol{u_1}, …, \boldsymbol{u_p}}$ is any orthogonal basis for $W$, then
\[\hat{\boldsymbol y} = \frac{\boldsymbol{u_1}\cdot \boldsymbol{y}}{\boldsymbol{u_1}\cdot \boldsymbol{u_1}}\boldsymbol{u_1} + \frac{\boldsymbol{u_2}\cdot \boldsymbol{y}}{\boldsymbol{u_2}\cdot \boldsymbol{u_2}}\boldsymbol{u_2} + \cdots + \frac{\boldsymbol{u_p}\cdot \boldsymbol{y}}{\boldsymbol{u_p}\cdot \boldsymbol{u_p}}\boldsymbol{u_p}\]and
\[\boldsymbol z = \boldsymbol y - \hat{\boldsymbol y}\]- Proof
${\boldsymbol{u_1}, …, \boldsymbol{u_p}}$가 $W$의 orthogonal의 basis이고, $\hat{\boldsymbol{y}} \in W$이기 때문에
\[\hat{\boldsymbol{y}} =c_1\boldsymbol{u_1}+\cdots + c_p\boldsymbol{u_p}\]를 만족해야 합니다. orthogonal basis의 성질을 이용하면
\[c_j = \frac{\boldsymbol{u_j}\cdot \boldsymbol{y}}{\boldsymbol{u_j}\cdot \boldsymbol{u_j}}\]인 것을 알 수 있습니다. 즉,
\[\hat{\boldsymbol y} = \frac{\boldsymbol{u_1}\cdot \boldsymbol{y}}{\boldsymbol{u_1}\cdot \boldsymbol{u_1}}\boldsymbol{u_1} + \frac{\boldsymbol{u_2}\cdot \boldsymbol{y}}{\boldsymbol{u_2}\cdot \boldsymbol{u_2}}\boldsymbol{u_2} + \cdots + \frac{\boldsymbol{u_p}\cdot \boldsymbol{y}}{\boldsymbol{u_p}\cdot \boldsymbol{u_p}}\boldsymbol{u_p}\]입니다. 두 번째로, $\boldsymbol{z} = \boldsymbol{y}-\hat{\boldsymbol{y}}$가 $W^\perp$에 속하는지 확인하기 위해,
\[\boldsymbol{z}\cdot\boldsymbol{u_j} = (\boldsymbol{y}-\hat{\boldsymbol{y}})\cdot\boldsymbol{u_j} = \boldsymbol{u_j}\cdot \boldsymbol{y} - \frac{\boldsymbol{u_j}\cdot \boldsymbol{y}}{\boldsymbol{u_j}\cdot\boldsymbol{u_j}}\boldsymbol{u_j}\cdot\boldsymbol{u_j} = \boldsymbol{u_j}\cdot \boldsymbol{y} - \boldsymbol{u_j}\cdot\boldsymbol{y} = 0\]이 성립하므로, $\boldsymbol{z}$는 $W$의 orthogonal basis에 있는 모든 벡터와 orthogonal합니다. 따라서
\[\boldsymbol{z} \in W^\perp\]를 만족합니다.
Theorem
Let ${\boldsymbol{u_1}, …, \boldsymbol{u_p}}$ be an orthogonal basis for a subspace $W$ of $\mathbb R^n$. For each $\boldsymbol{y}$ in $W$, the weights in the linear combination
\[\boldsymbol{y}=c_1\boldsymbol{u_1}+\cdots + c_p\boldsymbol{u_p}\]where $c_i = \frac{\boldsymbol{u_i}\cdot \boldsymbol{y} }{\boldsymbol{u_i} \cdot \boldsymbol{u_i}}\boldsymbol{u_i}$
In this case $proj_W \boldsymbol{y} = \boldsymbol{y}$
- Proof
$\boldsymbol y \in W$이므로, $\boldsymbol y$는 $W$의 basis 벡터의 linear combination으로 표현할 수 있습니다. 이 때 ${\boldsymbol{u_1}, …, \boldsymbol{u_p}}$는 orthogonal basis이므로
\[\boldsymbol{y}=\frac{\boldsymbol{u_1}\cdot\boldsymbol{y}}{\boldsymbol{u_1}\cdot\boldsymbol{u_1}}\boldsymbol{u_1}+\cdots \frac{\boldsymbol{u_p}\cdot\boldsymbol{y}}{\boldsymbol{u_p}\cdot\boldsymbol{u_p}}\boldsymbol{u_p}\]가 됩니다.
Theorem : The best approximation theorem
Let $W$ be a subspace of $\mathbb R^n$, let $\boldsymbol{y}$ be any vector in $\mathbb R^n$, and let $\hat{\boldsymbol{y}}$ be the orthogonal projection of $\boldsymbol{y}$ onto $W$. Then $\hat{\boldsymbol{y}}$ is the closest point in $W$ to $\boldsymbol{y}$, in the sense that
\[\|\boldsymbol{y}-\hat{\boldsymbol{y}}\|<\|\boldsymbol{y}-\boldsymbol{v}\|\]for all $\boldsymbol{v}$ in $W$ distinct from $\hat{\boldsymbol{y}}$
- Proof
이 때, $\boldsymbol{y}-\hat{\boldsymbol{y}}$는 $W$에 orthogonal하므로, $\boldsymbol{v}-\hat{\boldsymbol{y}}$에도 orthogonal합니다. 즉
\[\|\boldsymbol{y}-\boldsymbol{v}\|^2 = \|\boldsymbol{y}-\hat{\boldsymbol{y}}^2\| + \|\boldsymbol{v}-\hat{\boldsymbol{y}}\|^2\]가 됩니다. $|\boldsymbol{v}-\hat{\boldsymbol{y}}|\geq 0 $이므로
\[\|\boldsymbol{y}-\boldsymbol{v}\|^2\geq\|\boldsymbol{y}-\hat{\boldsymbol{y}}\|^2\]을 만족합니다. 즉
\[\|\boldsymbol{y}-\boldsymbol{v}\|\geq\|\boldsymbol{y}-\hat{\boldsymbol{y}}\|\]을 만족합니다.
Theorem
If ${\boldsymbol{u_1}, …, \boldsymbol{u_p}}$ is an orthonormal basis for a subspace $W$ of $\mathbb R^n$, then
\[\hat{\boldsymbol{y}} = (\boldsymbol{u_1}\cdot \boldsymbol{y})\boldsymbol{u_1} + \cdots + (\boldsymbol{u_p}\cdot \boldsymbol{y})\boldsymbol{u_p}\]If $U=\begin{bmatrix} \boldsymbol{u_1} & … & \boldsymbol{u_p} \end{bmatrix}$,
\[proj_W\boldsymbol{y} = U^TU\boldsymbol{y}\]for all $\boldsymbol{y}\in\mathbb R^n$
- Proof
는 다음과 같이 matrix와 벡터의 곱으로 나타낼 수 있습니다.
\[\begin{bmatrix}\boldsymbol{u_1} & \cdots & \boldsymbol{u_p}\end{bmatrix} \begin{bmatrix}\boldsymbol{u_1}\cdot\boldsymbol{y} \\ \vdots \\ \boldsymbol{u_p}\cdot\boldsymbol{y} \end{bmatrix}\]$\boldsymbol{u_j}\cdot\boldsymbol{y} =\boldsymbol{u_j}^T\boldsymbol{y}$이므로
\[\begin{bmatrix}\boldsymbol{u_1} & \cdots & \boldsymbol{u_p}\end{bmatrix} \begin{bmatrix}\boldsymbol{u_1}\cdot\boldsymbol{y} \\ \vdots \\ \boldsymbol{u_p}\cdot\boldsymbol{y} \end{bmatrix} = \begin{bmatrix}\boldsymbol{u_1} & \cdots & \boldsymbol{u_p}\end{bmatrix} \begin{bmatrix}\boldsymbol{u_1}^T\boldsymbol{y} \\ \vdots \\ \boldsymbol{u_p}^T\boldsymbol{y} \end{bmatrix} = \begin{bmatrix}\boldsymbol{u_1} & \cdots & \boldsymbol{u_p}\end{bmatrix} \begin{bmatrix}\boldsymbol{u_1}^T \\ \vdots \\ \boldsymbol{u_p}^T \end{bmatrix}\boldsymbol{y}\]가 되어
\[U =\begin{bmatrix}\boldsymbol{u_1} & \cdots & \boldsymbol{u_p}\end{bmatrix}\]일 때,
\[\hat{\boldsymbol{y}} = UU^T\boldsymbol{y}\]가 됩니다.

댓글남기기