6.7 Application : Linear regression
이번 포스트에서는 orthogonal projection의 응용인 linear regression(선형 회귀)에 대해서 알아보겠습니다.
1) Linear regression
(1) Linear regression
두 변수 간의 관계를 확인하고 싶을 때 데이터를 이용하여 관계를 확인할 수 있습니다. 예를 들어 다음과 같이 $x, y$변수에 대한 data가 $(x_1, y_1), …, (x_n, y_n)$으로 존재하고, 산점도가 다음과 같이 존재한다면
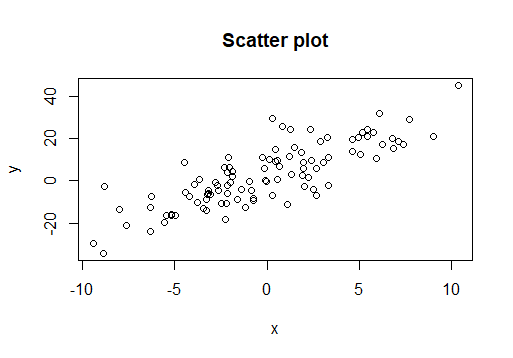
우리는 $x$와 $y$간 양의 상관관계를 가지고 있다고 생각할 수 있습니다. ($x$가 증가할 때 $y$도 증가하는 경향이 있습니다.) 그렇다면 $x$와 $y$간의 관계를 데이터를 이용하여 함수식으로 표현할 수 있을까요? 가장 간단한 함수인 일차함수를 생각해봅시다. 위 데이터를 이용하여
\[y=\beta_1x+\beta_0\]를 표현할 수 있다면 $x$와 $y$간의 관계를 수치적으로 이야기할 수 있고($x$가 1증가하면 $y$는 $\beta_1$만큼 증가합니다.), 임의의 $x$에 대해 $y$값을 예측할수도 있습니다.
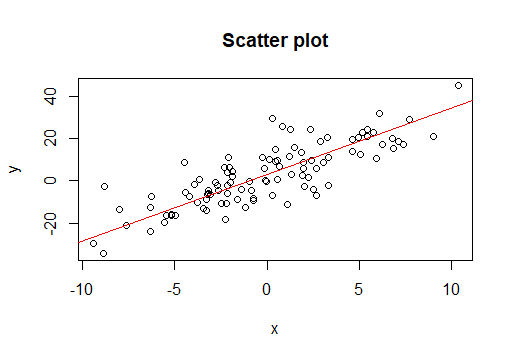
이를 시각적으로 표현하면 다음과 같습니다. 빨간색 직선의 기울기($\beta_1$)와 y절편($\beta_0$)이 우리가 구해야하는 값입니다.
(2) Notation and solution
data가 $(x_1, y_1), …, (x_n, y_n)$으로 있을 때 우리는
\[y=\beta_0 + \beta_1 x\]식에서 $\beta_0, \beta_1$을 구하는 것이 목표가 됩니다. 해당 data에 대해 위 식이 성립하므로
\[y_1 = \beta_0 + \beta_1x_1 +\epsilon_1\\ y_2 = \beta_0 + \beta_1x_2 +\epsilon_2\\ \vdots \\ y_n = \beta_0 + \beta_1x_n +\epsilon_n\]을 만족해야 합니다.(여기서 $\epsilon$은 error term입니다. 모든 데이터가 직선위에 존재하지 않기 때문입니다. 따라서 통제할 수 없는 오차 값을 따로 정의를 해줍니다.) 위 식을 생각해보면, $\beta_0, \beta_1$에 대한 linear system으로 생각할 수 있습니다. 이를 matrix로 표현하기 위해서 다음을 정의합니다.
\[Y=\begin{bmatrix}y_1 \\ y_2 \\ \vdots \\ y_n\end{bmatrix}, \ \ X=\begin{bmatrix}1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_n \end{bmatrix}, \ \ \boldsymbol \beta = \begin{bmatrix}\beta_0 \\ \beta_1\end{bmatrix}, \ \ \boldsymbol \epsilon =\begin{bmatrix} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_n \end{bmatrix}\]으로 정의하면, 위 linear system은
\[Y =X\boldsymbol \beta + \boldsymbol \epsilon\]가 됩니다. 만약 직선이 데이터를 잘 설명한다면,
\[Y \approx X\boldsymbol \beta\]가 만족되어야 합니다. 즉 $X\boldsymbol \beta$와 $Y$가 최대한 비슷해야 합니다. 비슷하다를 우리는 distance를 통해 정의를 하였습니다. 두 값이 비슷할수록
\[\|Y-X\boldsymbol{\beta}\|\]두 벡터 사이의 거리는 작아질 것입니다. 따라서, 위 데이터를 가장 잘 설명하는 직선($\boldsymbol{\beta}$)를 찾는 것은 두 벡터 사이의 거리를 최소화시키는 $\boldsymbol \beta$를 찾는 것과 같아집니다. 즉 least square problem을 푸는 것과 같아집니다.
\[\hat{\boldsymbol \beta} = \arg\min_{\boldsymbol \beta}\|Y-X\boldsymbol \beta\|\]이전 포스트에서, 해당 least sqaures problem의 solution은 다음의 equation을 푸는 것과 같다고 배웠습니다.
\[(X^TX)\boldsymbol \beta = X^TY\]만약 $X^TX$가 invertible하다면
\[\hat{\boldsymbol{\beta}} = (X^TX)^{-1}X^TY\]로 $\boldsymbol \beta$를 구할 수 있습니다.
(3) Extension : Multiple linear regression
$y$와 특정 변수 하나 $x$와의 관계 뿐만 아니라 여러 변수들 간의 관계를 나타내는 식을 구할수도 있습니다. 만약 데이터가
$(x_{11}, …, x_{1p}, y_1), (x_{21}, …, x_{2p}, y_2), …, (x_{n1}, …, x_{np}, y_n)$으로 주어져 있고, $y$와 각 변수간의 관계를 다음 식
\[y =\beta_0 +\beta_1x_1+\cdots + \beta_px_p\]으로 가정할 수 있습니다. 이 때, 우리가 구해야 하는 것은 $\beta_0, …, \beta_p$입니다.
해당 문제 또한 변수가 하나였을 때와 똑같은 방법을 적용할 수 있습니다. 다만 $X$ matrix와 $\boldsymbol \beta$ 벡터가 조금 달라집니다.
해당 데이터가 위의 식으로 표현되어야 하므로
\[y_i = \beta_0 + \beta_1x_{i1}+\cdots + \beta_px_{ip} +\epsilon_i, \ \ i=1,...,n\]으로 나타낼 수 있습니다. 이를 matrix로 표현하기 위해
\[Y=\begin{bmatrix}y_1 \\ y_2 \\ \vdots \\ y_n\end{bmatrix}, \ \ X=\begin{bmatrix}1 & x_{11} & \cdots & x_{1p} \\ 1 & x_{21} & \cdots & x_{2p} \\ \vdots & \vdots \\ 1 & x_{n1} & \cdots & x_{np} \end{bmatrix}, \ \ \boldsymbol \beta = \begin{bmatrix}\beta_0 \\ \beta_1 \\ \vdots \\ \beta_p\end{bmatrix}, \ \ \boldsymbol \epsilon =\begin{bmatrix} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_n \end{bmatrix}\]로 설정합니다. 이 경우 $Y\in \mathbb R^n, \ \boldsymbol{\beta}\in\mathbb R^p, \boldsymbol \epsilon\in \mathbb R^n$d이고, $X$는 $n \times p$ matrix가 됩니다. 해당 notation을 이용하면
\[Y =X\boldsymbol \beta + \boldsymbol \epsilon\]이 되고, 변수가 하나였을 때와 마찬가지로
\[\|Y-X\boldsymbol \beta\|\]를 최소화하는 $\boldsymbol{\beta}$가 solution이 되고 만약 $X^TX$가 invertible하면
\[\hat{\boldsymbol \beta} = (X^TX)^{-1}X^TY\]가 됩니다.
(3) Interpretation and Projection
위의 식을 이용하여 $\hat{\boldsymbol{\beta}}$를 구했다면 이 값을 통해 $Y$의 추정값(estimates)를 구할 수 있습니다.
\[\hat Y = X\hat{\boldsymbol{\beta}}\]가 됩니다. 이를 각 data별로 설명하면
\[\hat y_i = \hat \beta_0 + \hat \beta_1 x_{i1} + \cdots + \hat \beta x_{in}, \ \ i=1,...,n\]으로 표현됩니다. 해당 식의 의미를 확인하기 위해 least-sqaures problem을 살펴봅시다.
\[\|Y-X\boldsymbol \beta\|\]를 최소화시키는 $\boldsymbol \beta$가 least-squares solution이 됩니다. 이 때
\[X\boldsymbol\beta\]를 살펴봅시다. 위 식은 $X$의 column space에 속한 벡터입니다. 즉 임의의 벡터 $\boldsymbol{\beta}$에 대해서
\[X\boldsymbol \beta \in ColX\]를 만족합니다. 따라서 위 least squares problem은 $ColX$에서 $Y$와 가장 가까운 벡터를 만들어주는 $\boldsymbol{\beta}$를 찾는 문제가 됩니다. orthogonal projection의 성질에 의해 해당 조건을 만족하는 $\boldsymbol \beta$에 대해 $X\boldsymbol{\beta}$는 $proj_{ColX}Y$가 되는 것이구요. 따라서
\[\hat Y = X\hat{\boldsymbol \beta} = X(X^TX)^{-1}X^TY\]는 projection of $Y$ onto $ColX$가 됩니다. 여기서
\[H_X = X(X^TX)^{-1}X^T\]를 hat matrix 또는 projection matrix라고 합니다.
2) Weighted Least-Squares Problem
(1) Weighted Least-Squares Problem
Multiple linear regression에서의 least-squares problem
\[\|Y-X\boldsymbol \beta\|\]에서
\[\|Y-X\boldsymbol \beta\|^2\]을 풀어서 쓰면 다음과 같습니다.
\[\|Y-X\boldsymbol \beta\|^2 = \Sigma_{i=1}^n (y_i-(\beta_0+\beta_1x_{i1}+\cdots+\beta_px_{ip}))^2\]여기서 각 observation마다 직선 식과 실제 $y$값의 차이의 제곱을 모두 더한 값이 $|Y-X\boldsymbol \beta|^2$이 됩니다. 여기서 특정 observation이 다른 observation보다 중요하여, 가중치를 두는 상황이 발생할 수 있고, 반대로, 특정 observation이 부정확한 데이터여서, 해당 데이터에 대한 가중치를 낮추는 상황도 발생할 수 있습니다. 이 경우 해당 식을 다음과 같이 수정할 수 있습니다.
\[\Sigma_{i=1}^n w_i(y_i-(\beta_0+\beta_1x_{i1}+\cdots+\beta_px_{ip}))^2\]여기서 $w_i$가 가중치를 뜻하고, $w_i>0$을 만족합니다. 해당 식을 matrix로 표현하기 위해 다음 matrix
\[W = diag(w_1, ..., w_n)\]을 정의하면 해당 식은
\[\Sigma_{i=1}^n w_i(y_i-(\beta_0+\beta_1x_{i1}+\cdots+\beta_px_{ip}))^2 = (Y-X\boldsymbol \beta)^TW(Y-X\boldsymbol{\beta})\]로 표현할 수 있습니다. 여기서
\[W^{\frac{1}{2}} = diag(\sqrt{w_1}, ..., \sqrt{w_n})\]으로 설정하면($w_i>0$이므로 설정 가능합니다.) 위의 식은
\[(Y-X\boldsymbol \beta)^TW(Y-X\boldsymbol{\beta}) = \|W^{\frac{1}{2}}(Y-X\boldsymbol{\beta})\|^2\]이 됩니다. 다음과 같이
\[\|W^{\frac{1}{2}}(Y-X\boldsymbol{\beta})\|^2\]를 최소화시키는 $\boldsymbol \beta$를 찾는 문제를 Weighted-Least-Squares Problem이라고 합니다.
(2) Solving weighted-least-squares problem
Weighted-least-squares problem을 풀기 위해서 $\mathbb R^n$에서의 새로운 inner product를 정의합니다.
\[\langle \boldsymbol{x}, \boldsymbol{y} \rangle = \boldsymbol{x}^TW\boldsymbol{y}\]해당 연산은 inner product 성질을 만족합니다. (증명은 appendix 참고) 따라서 해당 inner product에 대해서 두 벡터 사이의 distance는
\[\|\boldsymbol{x}-\boldsymbol{y}\|_W^2 = (\boldsymbol{x}-\boldsymbol{y})^TW(\boldsymbol{x}-\boldsymbol{y})\]가 됩니다. 따라서 weighted-least-squares problem에서의 식은
\[(Y-X\boldsymbol \beta)^TW(Y-X\boldsymbol{\beta}) = \langle(Y-X\boldsymbol\beta), (Y-X\boldsymbol \beta) \rangle = \|Y-X\boldsymbol{\beta}\|_W^2\]다음과 같이 표현할 수 있습니다. 즉, $W$를 이용한 새로운 inner product space에서의 least-squares problem이 됩니다.
해당 문제의 solution을 $\hat{\boldsymbol \beta}$로 정의하면 $X\hat{\boldsymbol \beta}$는 $Y$의 $ColX$로의 orthogonal projection입니다. 따라서
\[(Y-X\hat{\boldsymbol \beta}) \perp_W ColX\]를 만족하고 이는 $X$의 column과 $Y-X\hat{\boldsymbol \beta}$가 orthogonal하므로 $X = \begin{bmatrix}\boldsymbol{x_1} & \cdots & \boldsymbol{x_p} \end{bmatrix}$인 $X$에 대해
\[(Y-X\hat{\boldsymbol \beta}) \perp_W \boldsymbol{x_j} \ \ for \ \ j =1,...,p\]이므로
\[\boldsymbol{x_j}^TW(Y-X\hat{\boldsymbol \beta})=0\]을 만족하므로
\[X^TW(Y-X\hat{\boldsymbol \beta}) = 0\]을 만족합니다. 따라서
\[X^TWX\hat{\boldsymbol \beta} = X^TWY\]를 만족합니다. 여기서 만약 $X^TWX$가 invertible하다면
\[\hat{\boldsymbol \beta} = (X^TWX)^{-1}X^TWY\]가 됩니다.
지금까지 orthogonal projection의 응용인 linear regression과 weighted least-squares problem에 대해 알아보았습니다. 다음 포스트에서는 inner product space의 응용인 fourier series에 대해 알아보겠습니다. 질문이나 오류 있으면 댓글 남겨주세요! 감사합니다!
Appendix : Weighted-Least-Squares
Property
For $\boldsymbol x, \boldsymbol y \in \mathbb R^n$, define $\langle\boldsymbol{x}, \boldsymbol{y} \rangle_W$ as
\[\langle\boldsymbol{x}, \boldsymbol{y} \rangle_W = \boldsymbol{x}^TW\boldsymbol{y}\]where
\[W=diag(w_1, ..., w_n). \ \ w_i>0 \ \ for \ \ i=1,...,n\]Then this operation satisfies inner product conditions.
- Proof
해당 연산이 inner product임을 밝히기 위해서는 4가지 조건을 밝혀야 합니다.
- $\langle\boldsymbol{x}, \boldsymbol{y} \rangle_W =\langle\boldsymbol{y}, \boldsymbol{x} \rangle_W$
첫 번째 조건은 성립합니다.
- $\langle\boldsymbol{x}+\boldsymbol{y}, \boldsymbol{z} \rangle_W=\langle\boldsymbol{x}, \boldsymbol{z} \rangle_W + \langle\boldsymbol{y}, \boldsymbol{z} \rangle_W$
두 번째 조건 또한 성립합니다.
- $\langle c\boldsymbol{x}, \boldsymbol{y} \rangle_W=c\langle\boldsymbol{x}, \boldsymbol{y} \rangle_W$, $c$ is scalar
세 번째 조건도 성립합니다.
- $\langle\boldsymbol{x}, \boldsymbol{x} \rangle_W\geq 0$, $\langle\boldsymbol{x}, \boldsymbol{x} \rangle_W=0$ if and only if $\boldsymbol{x}=0$
이는 $w_i>0$이므로 성립합니다. 또한 $w_i>0$이므로 해당 연산값이 0이 되려면
\[\langle\boldsymbol{x}, \boldsymbol{x} \rangle_W = 0 \iff \boldsymbol{x} =0\]이 되어야 합니다.
따라서 inner product가 되기 위한 4가지 조건을 만족하였으므로
\[\langle\boldsymbol{x}, \boldsymbol{y} \rangle_W = \boldsymbol{x}^TW\boldsymbol{y}\]는 inner product가 됩니다.

댓글남기기