7.5 Principal Component Analysis

이번 포스트에서는 Principal Component Analysis(주성분 분석)에 대해서 알아보겠습니다.

1) Principal Component Analysis

1) Basic Statistics

주성분분석을 하기에 앞서 기본적인 통계 용어와 개념이 필요합니다.

Definition : Mean, Variance, Covariance, Correlation coefficient

Given random variables $X, Y$, with pdf $f_X(x), f_Y(y)$, the mean of $X$ is (with $E(\begin{vmatrix} X \end{vmatrix})<\infty$)

\[E(X) = \begin{cases} \sum xf_X(x) & x : discrete \\ \int xf_X(x) & x : continuous\end{cases}\]

If $E(X^2)<\infty$ and $E(X)<\infty$, the variance of $X$ is

\[Var(X) = E[(X-E(X))^2]\]

If $E(X^2)<\infty, E(Y^2)<\infty, E(XY)<\infty$, the covariance of $X, Y$ is

\[Cov(X, Y) = E[(X-E(X))(Y-E(Y))]\]

and the correlation coefficient of $X$ and $Y$ is

\[Corr(X, Y) = \frac{Cov(X, Y)}{\sqrt{Var(X)}\sqrt{Var(Y)}}\]

확률 변수를 정의하고 확률분포를 알게 되면 평균(mean)과 분산(variance)을 구할 수 있습니다. 추가적으로, 두 개의 확률변수의 관계를 나타내는 값으로 공분산(covariance)과 상관계수(correlation coefficient) 정의할 수 있습니다.

하지만 우리는 데이터를 얻었을 때 전체 데이터(모집단이라고 합니다.)를 얻을 수 없기 때문에, 그 중 일부분을 추출한 데이터(표본)를 바탕으로 전체 데이터가 어떤 형태를 가지는지 추측을 합니다.

Definition : Sample mean, Sample variance, Sample covariance, Sample correlation coefficient, Sample Covariance matrix

Given the data $(x_1, y_1), (x_2, y_2), …, (x_n, y_n)$, the sample mean of $X$ and $Y$ is

\[\bar X = \frac{1}{n}\sum_{i=1}^n x_i, \ \ \bar{Y} = \frac{1}{n}\sum_{i=1}^ny_i\]

The sample variance of $X$ and $Y$ is

\[\hat{Var}(X) = \frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{X})^2, \ \ \hat{Var}(Y) = \frac{1}{n-1}\sum_{i=1}^n(y_i-\bar Y)^2\]

The sample covaraince of $X$ and $Y$ is

\[\hat{Cov}(X, Y) = \frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{X})(y_i-\bar{Y})\]

The sample correlation coefficient of $X$ and $Y$ is

\[\hat{Corr}(X, Y) = \frac{\hat{Cov}(X, Y)}{\sqrt{\hat{Var}(X)}\sqrt{\hat{Var}(Y)}}\]

표본 평균, 분산, 공분산, 상관계수에서 생각해야 하는 점은 다음과 같습니다.

1. 분산이 클수록 데이터가 sample mean에서 퍼져있고, 분산이 작을수록 데이터가 sample mean에 몰려있다.

   • Sample variance의 정의를 보면 데이터에서 데이터의 평균을 뺀 값들을 제곱하여 더한 뒤, sample 개수-1로 나눈 값입니다. 만약 데이터가 평균에 몰려있다면, 데이터에 평균을 뺀 값은 0에 가까울 것이고, 제곱을 하면 0에 가까운 값이 나올 것입니다. 따라서 이를 다 더한 뒤 특정 값으로 나눈 sample variance는 작은 값을 가집니다. 한편 데이터가 평균에서 퍼져있다면, 데이터에 평균을 뺀 결과가 큰 값들이 존재할 것이고, 이를 제곱하면 0에서 먼 값, 즉 상당히 큰 값이 나올 것입니다. 이를 더한 뒤 특정 값으로 나눈 sample variance는 큰 값을 가집니다.

2. Sample covariance가 양의 값을 가지면 두 변수는 양의 상관관계, 음의 값을 가지면 두 변수는 음의 상관관계를 가진다.

   • Sample covariance는 두 데이터 간의 관계를 나타내주는 값입니다. $x_i$가 $\bar X$보다 클 때, $y_i$는 $\bar Y$보다 클 수도, 작을 수도 있습니다. 다음의 그림과 같이 데이터의 위치에 따라 4 가지 경우로 나눌 수 있습니다.

     

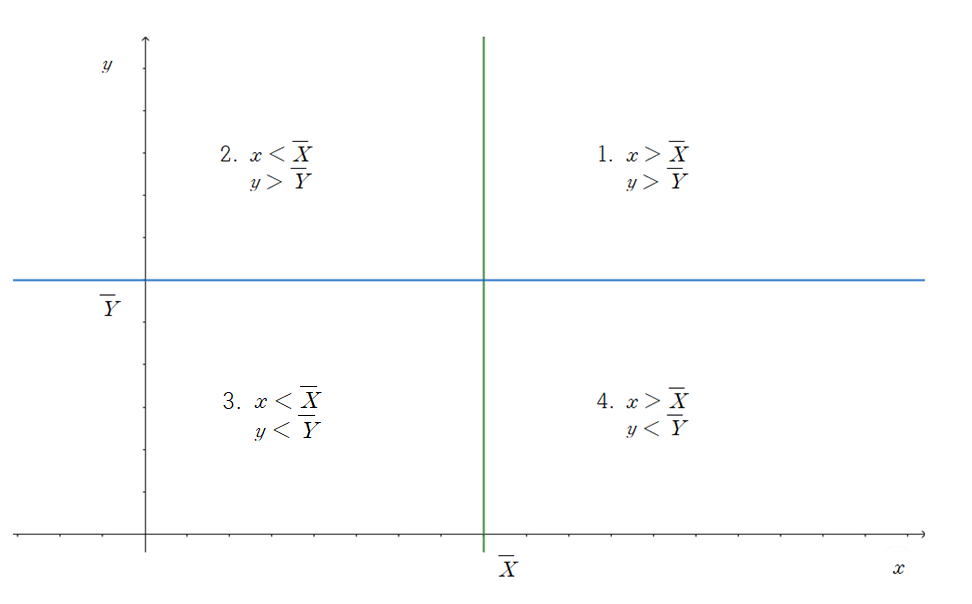
     만약 데이터가 1과 3 부분에 많이 존재한다면, sample covariance 계산 식인 $(x_i-\bar X)(y_i-\bar Y)$ 값은 양수가 될 것입니다. 따라서 이를 다 더하고 sample 개수-1로 나눈 값 또한 양수가 될 것입니다. 1번과 3번 부분에 데이터가 많이 존재한다는 것은, $X$가 증가할 때 $Y$도 증가한다는 것을 의미합니다. 따라서 양의 상관관계를 가진다고 할 수 있습니다.

     두 번째로, 데이터가 2번과 4번 부분에 많이 존재한다면, sample covariance 계산 식 값은 음수가 될 것입니다. 이를 다 더하고 sample 개수-1로 나눈 값 또한 음수가 됩니다. 2번과 4번 부분에 데이터가 많이 존재한다는 것은 $X$가 증가할 때 $Y$는 감소하는 것을 의미합니다. 따라서 음의 상관관계를 가진다고 할 수 있습니다.

     마지막으로 데이터가 1, 2, 3, 4에 고르게 분포할 경우, sample covariance의 값은 0에 근접한 값을 가지게 됩니다.

3. Sample correlation coefficient는 상관관계 강도까지 나타낸 값으로, -1과 1에 가까울수록 강한 상관관계를 가진다.

   • Sample correlation은 sample covariance에 각 변수의 sample variance의 root값을 나눈 값으로, 최소 -1에서 최대 1의 값을 가지게 됩니다. Sample covaraince에서는 단순히 양의 상관관계가 있는지, 음의 상관관계가 있는지만을 확인할 수 있었다면, Sample correlation coefficient는 그 강도가 얼마나 강한지까지 알 수 있는 지표입니다. 1에 가까울수록 강한 양의 상관관계(기울기가 양수인 직선 형태), -1에 가까울수록 강한 음의 상관관계(기울기가 음수인 직선형태)를 띄게 됩니다.

     마지막으로, correlation coefficient가 0인 경우, 두 변수는 uncorrelated이다고 정의합니다.

(2) Data and Dimension

Principal Component Analysis(PCA)의 목적은 dimension을 줄이는데 있습니다. 그렇다면 데이터를 분석하는데 있어 dimension을 줄이는 이유는 무엇인지, 줄였을 때 어떤 효과를 얻을 수 있는지 알아보겠습니다.

데이터를 설명하는 변수가 많아질 때 우리가 가질 수 있는 이점은 무엇일까요? 변수가 추가될 때 마다 현재 데이터가 가지는 정보를 설명해주기 때문에, 변수가 많아지면 많아질수록 우리가 데이터로부터 얻을 수 있는 정보는 많아집니다.

그렇다고 데이터를 설명하는 변수가 많아진다고 해서 좋은 점만 있는 것은 아닙니다. 변수가 많을수록 변수를 통제하거나 데이터에서 해당 변수가 가지는 의미를 설명하기가 어려워집니다. 다음 두 식을 살펴봅시다.

\[y = \alpha_0 + \alpha_1 x_1 \ \cdots \ 1. \\ y = \beta_0 + \beta_1 x_1 +\beta_2 x_2 \ \cdots 2.\]

1번 식보다 2번 식이 $y$를 설명하는 변수가 하나 더 많습니다. $x_2$라는 변수 또한 $y$를 설명하는데 사용이 되었기 때문에, 2번 식이 1번 식보다 $y$에 대한 정보가 많다고 생각할 수 있습니다.

그렇다면 $x_1, x_2$가 $y$에 어떠한 영향을 주는지 해석해보겠습니다. 1번 식의 경우 간단히,

• $x_1$이 1 증가하면 $y$는 $\alpha_1$만큼 증가한다.

와 같이 해석할 수 있습니다. 하지만, 2번 식의 경우 1번 식과 같이 해석을 할 수 없습니다. $\beta_2 x_2$이 존재하기 때문입니다. 따라서 $x_1$이 $y$에 주는 영향을

• $x_2$가 고정이 되었을 때, $x_1$이 1 증가하면 $y$는 $\beta_1$만큼 증가한다

로 해석해야 합니다. 부가적인 조건이 붙게 됩니다.

이처럼 변수가 무작정 많아진다고 해서 좋은 것도 아니고, 엄청 적다고 해서 좋지는 않습니다. 데이터를 설명하는 적절한 변수 개수와 적당한 변수를 선택하는 문제는 통계학/머신러닝에서 중요한 문제 중 하나입니다.

그럼 내가 원하는 변수를 내가 원하는 개수만큼 선택해서 분석을 진행하면 되지 않나? 생각을 할 수 있습니다. 하지만 무작정 자신이 원하는 변수나 변수 개수를 선택하면 문제가 발생할 수 있습니다.

다음의 두 데이터 분포를 봅시다.

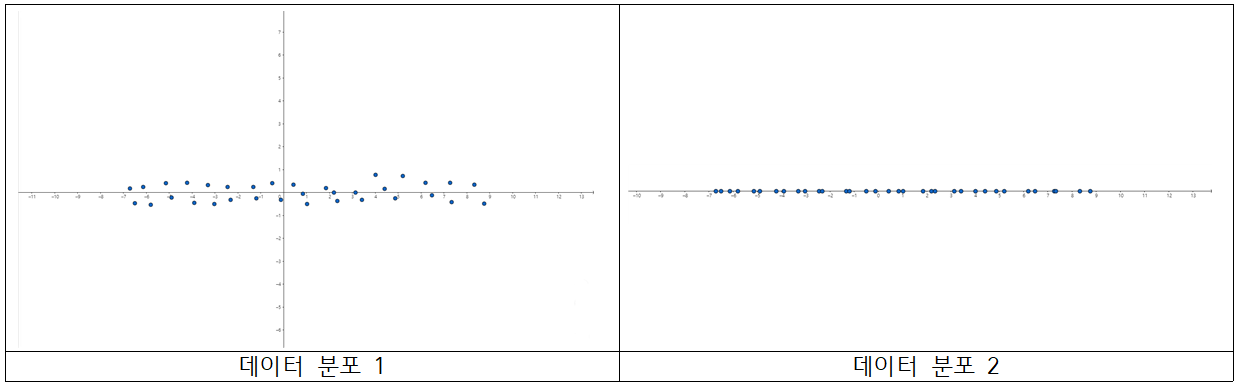
변수 $X, Y$에 대한 데이터 분포입니다. 첫 번째 분포는 $X, Y$ 두 변수 모두를 고려하여 산점도를 그렸습니다.(가로축 : $x$축, 세로축 : $y$축) 그리고 두 번째 분포는 $X$ 변수만 고려하여 산점도를 그렸습니다.(가로축 : $x$축) 즉 데이터 분포 1에서의 x좌표만 나타낸 분포가 데이터 분포 2입니다.

데이터 분포 1을 살펴봅시다. 현재 $X$변수는 고르게 퍼져있고, $Y$ 변수는 0에 근접한 값들이 많습니다. 이를 다시 말하면, $X$ 변수는 상대적으로 분산(또는 표본 분산)이 크고, $Y$ 변수는 상대적으로 분산이 작은 것을 알 수 있습니다.

데이터 분포 1과 2를 비교해봅시다. 데이터의 경향성에 큰 변화가 있다고 느껴지시나요? $Y$값들이 0 근처의 값에 몰려 있다 보니, 굳이 $Y$값을 사용하지 않더라도 데이터 경향성(정보)에 큰 변화가 없습니다.

그렇다면 다음 데이터 분포를 살펴봅시다.

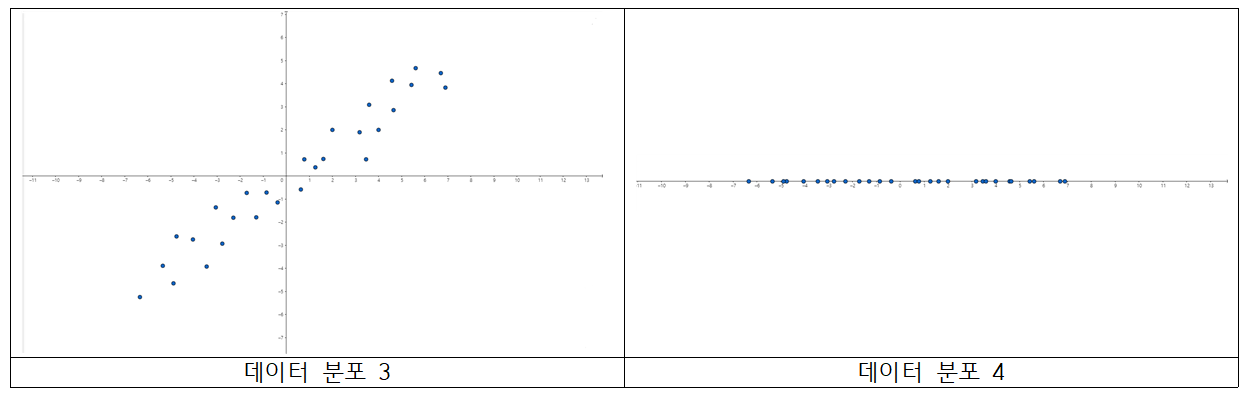
세 번째 분포가 첫 번째 분포와 조금 다릅니다. 똑같이 세 번째 분포는 $X, Y$ 두 변수를 모두 고려하여 산점도를 그렸고(가로축 : $x$축, 세로축 : $y$축) 네 번째 분포는 $X$ 변수만 고려하여 산점도를 그렸습니다.(가로축 : $x$축) 마찬가지로 데이터 분포 3에서 x좌표만 나타낸 분포가 데이터 분포 4입니다.

데이터 분포 3을 보면 $X, Y$ 각각 평균에서 떨어진 값들이 존재합니다. 따라서, 두 변수 모두 분산이 큰 값을 가진다고 해석할 수 있습니다. 여기서 포인트는 $Y$ 값 또한 분산이 높다는 것입니다.

데이터 분포 3과 4를 비교해봅시다. 경향성에 큰 차이가 있는 것이 보이시나요? 데이터 분포 3의 경우 기울기가 양의 값을 가지는 직선 형태의 분포를 가지는 반면, 데이터 분포 4는 x축 직선 모양을 가집니다.(물론 $Y$값을 제거했으니 당연한 이야기입니다.) 중요한 점은, 데이터를 설명하는 변수 중 $Y$ 또한 많은 정보를 담고 있는 것입니다. $Y$값이 0에서 멀리 떨어진 데이터의 $Y$ 값을 전부 무시하고 데이터 분포 4를 만들었으니, 데이터 경향성에 큰 변화가 생긴 것을 알 수 있습니다. 이런 경우 데이터의 정보 손실이 많아져 합리적인 분석을 하는데 문제가 발생합니다.

위와 같이 두 개의 변수 뿐만 아니라, 수십개, 수백개의 변수 중에서 위와 같은 경우가 존재할 수 있습니다. 무턱대고 변수를 제거하면 데이터 정보의 큰 손실을 초래할 수 있습니다. PCA는 데이터의 정보의 손실을 최소화하면서, 변수 개수를 줄일 수 있는 방법론 중 하나입니다.

(3) Idea of PCA

PCA는 선형 대수의 지식을 이용하여 데이터 분포 3을 데이터 분포 1처럼 보이게 만들어주는 작업입니다. 그럼 어떤 방법을 이용하여 데이터 분포 3을 데이터 분포 1로 바꾸어주는지 확인해 봅시다.

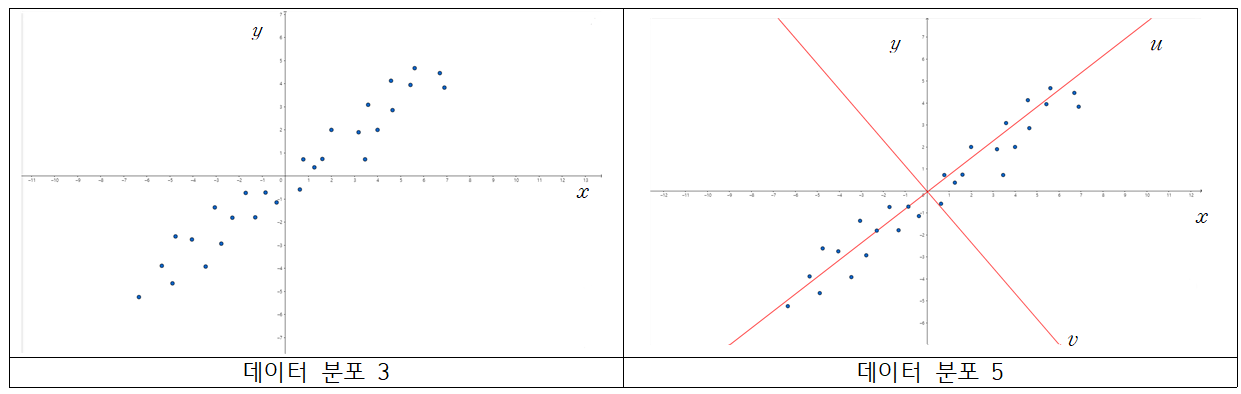
데이터 분포 3을 다시 봅시다. 현재 $X, Y$ 변수 사이 양의 상관관계가 있는 것을 알 수 있습니다. PCA는 여기서 새로운 축을 생성을 합니다. 새로운 축을 형성할 때, 새로운 축 변수의 분산이 가장 크도록 생성을 해줍니다. 데이터 분포 5에서 $u$ 축이 해당 조건을 만족하는 새로운 변수이고, 축입니다. 두 번째는 $u$ 축과 수직이면서, 그 다음으로 축 변수의 분산이 가장 크도록 생성을 해줍니다. 데이터 분포 5에서 $v$ 축이 해당 조건을 만족하는 새로운 변수이고, 축입니다.

이 후, $x, y$축, 또는 $X, Y$ 변수가 아닌, 새로운 축인 $u, v$축, 또는 $U, V$ 변수를 이용하여 데이터를 해석합니다. 그 결과가 아래의 데이터 분포가 됩니다.

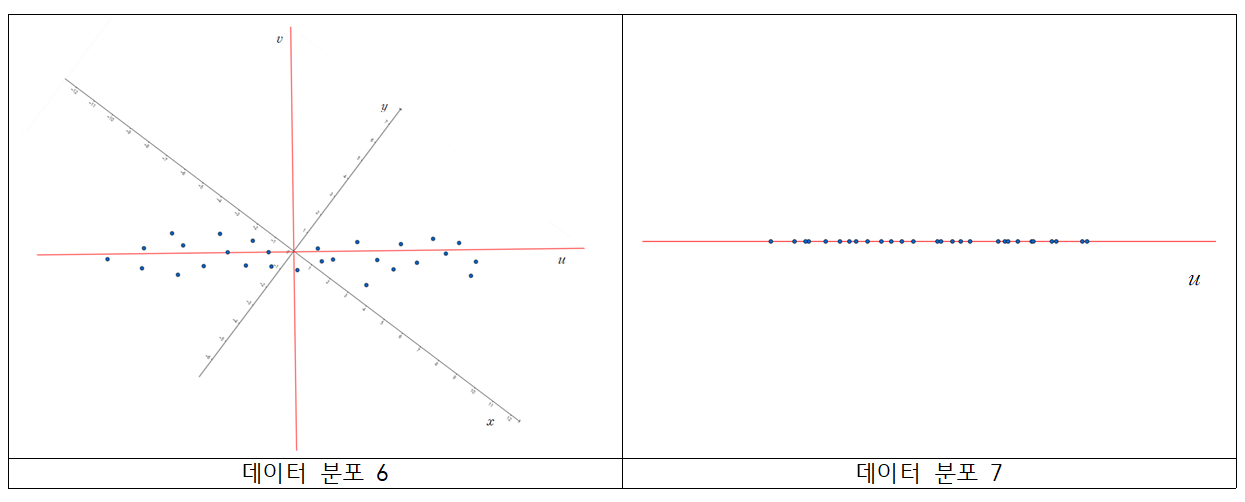
데이터 분포 6은 데이터 분포 5에서 $u$축과 $v$축을 기준으로 하기 위해 회전시킨 산점도이고, 데이터 분포 7은 $U, V$ 중 $U$ 변수만 고려하여 그린 산점도입니다. 데이터분포 1, 2와 같은 형태를 띄는 것이 보이시나요? $V$ 변수의 분산이 작기 때문에, $V$ 변수가 가지는 데이터 정보가 적어서, $V$를 제거하고 $U$만 고려해도 데이터 정보의 손실이 적은 것을 알 수 있습니다.

정리하면, Principal Component Analysis(PCA)는 데이터의 분산을 가장 크게 만드는 축을 찾고, 그 축과 수직이면서 그 다음으로 분산이 큰 축들을 차례대로 찾아주는 방법입니다. 이 후 분산이 작은 축들은 제거를 해도 데이터 정보의 손실이 적고, 해석하기도 용이해집니다.

2) Derivation of PCA

그럼 어떤 방법으로 분산이 가장 큰 축을 찾는지 수식으로 확인해 봅시다.

(1) Covariance matrix

위에서 시각적 표현을 쉽게 하기 위해 변수 2개만 사용하였지만, 실제로는 변수의 개수가 많을 수 있습니다. 따라서 변수의 개수가 $p$일 때 변수간의 관계를 설명하기 위해 벡터와 matrix를 사용합니다.

Notation

Given the random variable $X_1, …, X_p$, the covariance matrix is

\[\begin{bmatrix} Var(X_1) & Cov(X_1, X_2) & \cdots & Cov(X_1, X_p) \\ Cov(X_2, X_1) & Var(X_2) & \cdots & Cov(X_2, X_p) \\\vdots & \vdots & \ddots & \vdots & \\ Cov(X_p, X_1) & Cov(X_p, X_2) & \cdots & Var(X_p)\end{bmatrix}\]

Given the data $(x_{11}, …, x_{1p}), …, (x_{n1}, …, x_{np})$, we can set $n\times p$ matrix

\[X = \begin{bmatrix} x_{11} & ... & x_{1p} \\ \vdots & \ddots & \vdots \\ x_{n1} & \cdots & x_{np} \end{bmatrix}\]

If we set the sample mean

\[\bar X_{j} = \frac{1}{n}\sum_{i=1}^nx_{ij}, \ \ j=1,...,p\]

then the sample covariance matrix is

\[\hat {Cov}(\boldsymbol X) = \begin{bmatrix} \hat{Var}(X_1) & \hat{Cov}(X_1, X_2) & \cdots & \hat{Cov}(X_1, X_p) \\ \hat{Cov}(X_2, X_1) & \hat{Var}(X_2) & \cdots & \hat{Cov}(X_2, X_p) \\\vdots & \vdots & \ddots & \vdots & \\ \hat{Cov}(X_p, X_1) & \hat{Cov}(X_p, X_2) & \cdots & \hat{Var}(X_p)\end{bmatrix}\]

여러 개의 변수에 대해 sample mean과 sample variance, sample covariance를 정의할 수 있고, 이를 matrix 형태로 나타낸 것이 sample covariance matrix입니다.

$X$에서 각각의 변수에 sample mean을 뺀 새로운 matrix를 $\tilde X$

\[\tilde X = \begin{bmatrix} x_{11}-\bar X_1 & ... & x_{1p}-\bar X_p \\ \vdots & \ddots & \vdots \\ x_{n1}-\bar X_1 & \cdots & x_{np}-\bar X_p \end{bmatrix}\]

로 정의하면 sample covariance matrix는

\[\hat{Cov}(\boldsymbol X) = \frac{1}{n-1}\tilde X^T\tilde X\]

가 됩니다.

이제 이 covariance matrix를 적절하게 변형시켜, variance 항만 살아있고, 나머지 covariance항은 0이 되도록 변형시킬 예정입니다.

(2) Spectral Decomposition

지금 sample covariance matrix에서 $\tilde X^T\tilde X$를 보면 symmetric matrix입니다. 따라서, 해당 matrix는 orthogonally diagonalizable합니다. 즉

\[\tilde X^T \tilde X = PDP^T\]

로 분해가 가능합니다.

여기서, 새로운 변수(새로운 축을 담당합니다.) $Y$를

\[Y = \tilde XP\]

로 설정을 하면

\[\frac{1}{n-1}Y^TY = \frac{1}{n-1}P^T\tilde X^T\tilde XP = \frac{1}{n-1}P^TPDP^TP = \frac{1}{n-1}D\]

가 되어, 새롭게 표현한 데이터 $Y$ 변수간 sample covariance matrix가 diagonal matrix가 됩니다. 즉, 현재 $Y$ 또한 $n\times p$ matrix, 즉 변수가 $p$개 존재하는데, $p$개의 변수간 sample covariance가 모두 0이 됩니다. 이 때 $D$의 diagonal element가 variance가 되구요.

(3) New Axis

$Y$가 가지는 의미에 대해서 알아봅시다. $Y$는 $n\times p$ matrix로

\[Y = \tilde XP \\ \Rightarrow \tilde X = YP^T\]

를 만족합니다. 여기서 양변에 transpose를 취하면

\[\tilde X ^T = PY^T\]

가 됩니다. $\tilde X^T$는 $p \times n$ matrix로

\[\tilde X^T = \begin{bmatrix}\tilde x_{11} & \tilde x_{21} & \cdots & \tilde x_{n1} \\ \tilde x_{12} & \tilde x_{22} & \cdots & \tilde x_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ \tilde x_{1p} & \tilde x_{2p} & \cdots & \tilde x_{np} \end{bmatrix}\]

각각의 column이 data, observation 역할을 합니다. 이 때, $P = p\times p$ matrix로

\[P = \begin{bmatrix}\boldsymbol p_1 & \boldsymbol p_2 & ... & \boldsymbol p_p \end{bmatrix}\]

로 표현할 수 있습니다. 위의 $\tilde X^T$의 첫 번째 column을 $P, Y$로 나타내면

\[\begin{bmatrix}\tilde x_{11} \\ \tilde x_{12} \\ \vdots \\ \tilde x_{1p} \end{bmatrix} = P\begin{bmatrix}y_{11} \\ y_{12} \\ \vdots \\ y_{1p} \end{bmatrix} = y_{11}\boldsymbol p_1 + y_{12}\boldsymbol p_{2} + \cdots + y_{1p}\boldsymbol p_p\]

가 됩니다. 즉, $\tilde X^T$의 첫 번째 column, 첫 번째 observation을 standard basis가 아닌 $P$의 column으로 이루어진 basis를 통하여 표현하였을 때의 coordinate vector가 $Y^T$의 첫 번재 column이 됩니다.

이를 확장하면 $\tilde X^T$의 $j$번째 column, $j$번째 observation을 standard basis가 아닌 $P$의 column을 이루어진 basis를 통하여 표현하였을 때의 coordinate vector가 $Y^T$의 $j$번째 column입니다.

따라서 PCA idea 설명 부분에서 만든 새로운 축이라는 뜻은 **$P$의 column을 basis로 하였을 때 $\mathbb R^p$를 표현하는 축입니다. **

(4) Meaning of eigenvalue and eigenvector

$\tilde X^T \tilde X$를 spectral decomposition(또는 diagonalization)을 통해 $PDP^T$로 분해하여, 새로운 변수 $Y$를 만들었습니다. spectral decomposition을 진행할 때 $\tilde X^T \tilde X$의 eigenvalue와 eigenvector를 이용하는데, PCA의 결과로 얻은 새로운 축과 eigenvalue, eigenvector간 관계에 대해 알아봅시다.

\[\tilde X^T \tilde X = PDP^T\]

로 분해할 수 있고

\[P = \begin{bmatrix} \boldsymbol p_1 & ... & \boldsymbol p_p \end{bmatrix}, \ \ D = diag(\lambda_1, ..., \lambda_p)\]

입니다. 여기서 $\lambda_1, …, \lambda_p$는 $\tilde X^T \tilde X$의 eigenvalue이고, $\boldsymbol p_1, …\boldsymbol p_p$는 각각의 eigenvalue에 해당하는 크기 1의 eigenvector입니다.

\[Y = \tilde XP\]

로 설정하였을 때, $Y$를 이루는 변수의 sample covariance matrix

\[\frac{1}{n-1}Y^TY = \frac{1}{n-1}D\]

의 diagonal term이 eigenvalue로 이루어져 있습니다. 즉 $Y$의 각 축들의 variance를 $n-1$로 곱한 값이 $\tilde X^T\tilde X$의 eigenvalue입니다.

다음은 eigenvector입니다. $Y$는 $\tilde X$를 $P$의 column을 basis를 이용하여 표현하였을 때의 coordinate vector들을 모아놓은 matrix입니다. 따라서 $P$의 column은 $\mathbb R^p$를 나타내는 새로운 축으로 생각할 수 있습니다. 그런데 $P$는

\[P = \begin{bmatrix} \boldsymbol p_1 & ... & \boldsymbol p_p \end{bmatrix}\]

이고, column 모두 eigenvector이므로, $\tilde X^T \tilde X$의 eigenvector는 PCA를 진행한 후 생성되는 새로운 축을 의미합니다. 그 새로운 축에 대한 분산이 eigenvector에 대응하는 eigenvalue에 $n-1$을 나눈 값이 되구요.

(5) Dimension reduction

마지막으로 실제로 차원을 낮추는 단계입니다. $\tilde X^T \tilde X$의 eigenvalue가 해당 축의 variance에 비례하는 것을 이용하여, variance 비교를 통해 필요없는 변수를 제거하는 과정을 거칩니다. 하지만 variance가 작다는 것을 어떻게 정의할까요? 이를 위해 condition number를 정의합니다.

Definition : Condition number

If $\lambda_1, …, \lambda_p$ are eigenvalue of $\tilde X^T \tilde X$, then the condition number of $j$th variable is

\[\frac{\lambda_j}{\sum_{i=1}^p\lambda_i}\]

Condition number는 전체 variance 대비 각 변수별 variance 비율을 나타내는 값입니다. condition number가 클 수록, 해당 축의 variance가 크다는 것을 의미합니다. 따라서 이 값이 작은 변수는 제거함으로써 dimension reduction을 진행할 수 있습니다.

두 번째로, Scree plot을 통해 적절한 변수 개수를 선택할 수 있습니다. PCA를 진행할 때, 분산이 최대가 되도록 축을 생성합니다. 따라서 축이 추가될 때마다 해당 축의 분산은 작아집니다. 따라서 x축을 축 index, y축을 해당 축에 대한 condition number(또는 cummulated condition number)를 지정하여 꺾은선 그래프를 만들 수 있습니다. 이러한 꺾은선 그래프를 Scree plot이라고 합니다.

Scree plot에서 기울기가 완만해지는 지점의 변수 개수를 최적의 변수개수로 지정하여 분석을 진행할 수 있습니다.

지금까지 Principal Component Analysis에 대해서 알아보았습니다. 이번 포스트까지 해서 학부에서 배울 수 있는 선형 대수학에 대한 기본적인 지식 포스트가 완료 되었습니다. 추가적으로 다른 포스트에서 선형대수와 관련이 있는 내용을 다룰 때 추가적으로 포스트할 예정입니다. 질문이나 오류 있으면 댓글 남겨주세요! 감사합니다!